Übung 6

Path Rotation Task - Daten aus dem Online Experiment.

true
06-21-2021

Hintergrund

Mentale Rotation, also das Drehen von Gegenständen, Personen oder unserer eigenen Position mittels der eigenen Vorstellungskraft, ist eine wichtige Fähigkeit von Menschen. Sie ermöglicht es uns die Perspektive zu wechseln, uns vorzustellen, wie wir ein Problem lösen können und Werkzeuge zu benutzen. Wir verwenden mentale Rotation beispielsweise um einem Freund den Weg aus seiner Sicht zu erklären oder um die Anleitung zum Zusammenbau eines Möbels zu verstehen. Mentale Rotationsaufgaben beanspruchen das räumliche Arbeitsgedächtnis und können, wie folgende Grafik zeigt, ganz unterschiedlich aussehen:

Experimentalparadigmen zum Untersuchen von Mentaler Rotation. (A) Shepard-Metzler Figuren (Shepard & Metzler, 1971) (B) Koerper-, Hand- oder Buchstabenstimuli (Falconer & Mast, 2012) (C) Path Rotation Stimuli aus dem Online Experiment.

Figure 1: Experimentalparadigmen zum Untersuchen von Mentaler Rotation. (A) Shepard-Metzler Figuren (Shepard & Metzler, 1971) (B) Koerper-, Hand- oder Buchstabenstimuli (Falconer & Mast, 2012) (C) Path Rotation Stimuli aus dem Online Experiment.

Mentale Rotation kann mit unterschiedlichen Strategien ausgeführt werden: Man kann sich selber mental rotieren (egozentrische Rotation) oder ein Objekt (allozentrische Rotation). Diese Strategien beruhen auf unterschiedlichen Referenzsystemen im Gehirn und unterscheiden sich auf neuronaler Ebene (Tomasino and Gremese 2016).

Bestimmte Patientengruppen wie beispielsweise Kinder mit ADHD oder Patienten mit Erkrankungen des Gleichgewichtorgans (vestibuläre Patienten) zeigen im Vergleich zu Kontrollgruppen schlechtere Leistungen in mentalen Rotationsaufgaben (z.B.(Feldman and Huang-Pollock 2020; Grabherr et al. 2011)). Interessanterweise unterscheiden sich vestibuläre Patienten aber nur in der egozentrischen nicht in der allozentrischen Strategie von der Kontrollgruppe.

Dies wirft die Frage auf, wie die Information aus dem Gleichgewichtsorgan das Ausführen von mentalen Rotationen beeinflusst. Dieser Einfluss wurde in zahlreichen Experimenten im Labor und auch im Magnetresonanztomographen (MRT) untersucht. Für die fMRT Studien wurden meist je nach Strategie unterschiedliches Stimulus-Material verwendet, was es schwierig macht die Fehler, Reaktionszeiten sowie die Hirnaktivierungen in den beiden Strategien direkt zu vergleichen. Bei gleichem Stimulusmaterial besteht die Problematik, dass oft nicht klar ist, welche Strategie gewählt wurde.

Ein gutes Paradigma (bestehend aus Aufgabe, Stimulusmaterial, Timing und Instruktion) ist fundamental wichtig für neurowissenschaftliche Experimente. Es sollte den Prozess den wir untersuchen wollen auslösen und messbar machen. Dies ist oft schwieriger als es tönt. Das Erstellen, Optimieren und Austesten eines Paradigmas ist ein wichtiger Teil der Arbeit eines Neurowissenschaftlers.

Path Rotation Experiment

In diesem Experiment wurde eine mentale Rotationsaufgabe mit zwei verschiedenen Strategien gelöst. In beiden Strategien muss entweder mit rechts oder links geantwortet werden. Das Stimulusmaterial wurde so hergestellt, dass die Stimuli für beide Strategien visuell identisch sind, aber die Antwort aufzeigt, mit welcher Strategie die Aufgabe gelöst wurde.

  1. Die allozentrische Strategie erfordert das Drehen des Bildes, so dass der kurze Weg nach oben zeigt. Dann muss die Versuchsperson entscheiden, ob der Pfeil zur rechten oder zur linken Seite zeigt. Die egozentrische Strategie hingegen erfordert das Drehen der eigenen Perspektive.

  2. Die egozentrische Strategie erfordert das Drehen der eigenen Perspektive, so dass vom kurzen Pfadstück aus beurteilt werden kann, in welche Richtung der Weg an der Kreuzung abbiegt Richtung Pfeil.

Fragestellungen

Das Ziel dieser Onlinestudie ist es das neue Stimulusmaterial zu validieren. Hierfür interessieren uns folgende Fragen:

  1. Erhöhen sich die Antwortzeiten mit zunehmendem Rotationswinkel?

  2. Unterscheiden sich die Antwortzeiten zwischen den beiden Bedingungen in typischer Weise (egozentrisch schneller als allozentrisch)?

  3. Eignet sich dieses Paradigma für den Vergleich der Strategien in einem fMRI Experiment?

Daten laden

library(tidyverse)
library(viridis)

# ggplot Optionen
theme_set(theme_grey(base_size = 14) +
            theme(panel.grid = element_blank()))

Wir laden den Datensatz mit folgende Informationen:

Alter, Geschlecht und Händigkeit wurden aus Datenschutzgründen aus dem Datensatz entfernt. Wir laden die Variablen id, condition sowie die absoluten Winkelwerte (d.h. 45° links und 45° rechts werden aggregiert) fc_angle als Faktoren und schauen uns kurz den Datensatz an:

pathrotation <- read_csv("https://raw.githubusercontent.com/kogpsy/neuroscicomplab/main/data/PathRotation.csv") %>%
  mutate(id = as_factor(id),
         condition = as_factor(condition),
         fc_angle = as_factor(abs(angle)))

glimpse(pathrotation)

Rows: 8,665
Columns: 7
$ id        <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ condition <fct> egocentric, egocentric, egocentric, egocentric, eg…
$ angle     <dbl> -45, -135, 180, 90, -135, 90, -135, 45, -90, -90, …
$ rt        <dbl> 1660, 2717, 1734, 1329, 1435, 1420, 1387, 1319, 16…
$ accuracy  <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1,…
$ trial     <dbl> 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …
$ fc_angle  <fct> 45, 135, 180, 90, 135, 90, 135, 45, 90, 90, 45, 90…

Data Cleaning

Schliessen Sie alle Versuchspersonen aus, welche nicht das ganze Experiment durchgeführt haben.

# find id numbers of complete datasets
exclusion_incomplete <- pathrotation %>% 
  group_by(id) %>% 
  count() %>%
  filter(n == max(n))

# keep complete datasets in dataframe
pathrotation <- pathrotation %>%
  filter(id %in% exclusion_incomplete$id)

Schliessen Sie alle Versuchspersonen aus, welche in mindestens einer der Bedingungen über 25% der Trials falsch beantwortet haben (50% ist Rateniveau). Die Aufgabe kann erfahrungsgemäss relativ korrekt gelöst werden. Die Versuchspersonen wurden instruiert, möglichst richtig (nicht möglichst schnell) zu antworten, deshalb weist eine Accuracy von weniger als 75% auf falsches Verständnis der Instruktion hin.

# find id numbers of complete datasets
exclusion_rt <- pathrotation %>% 
  group_by(id, condition) %>% 
  summarize(mean_acc = mean(accuracy)) %>%
  filter(mean_acc >= 0.75)

# keep complete datasets in dataframe
pathrotation <- pathrotation %>%
  filter(id %in% exclusion_rt$id)

Schauen Sie sich die Antwortzeiten an, insbesondere die maximale Zeitdauer. Was fällt Ihnen auf?

# bar plot
pathrotation %>% 
  ggplot(aes(rt, fill = condition)) +
  geom_histogram(alpha = 1.0, position = "identity", color = "black") + 
  scale_fill_viridis(discrete=TRUE, option="cividis") +
  facet_grid(fc_angle ~ condition, scales = "free_x") +
  theme(legend.position = "none")

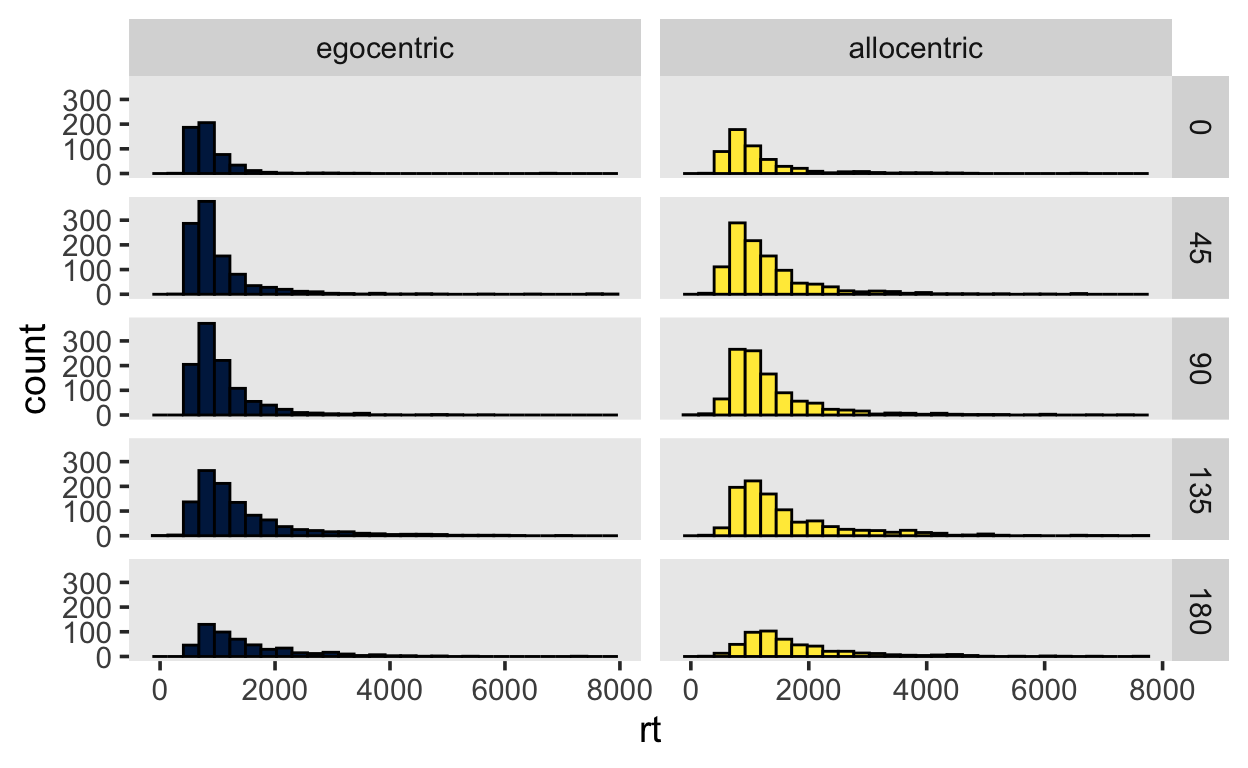
Teilweise hatten die Versuchspersonen bis 8 Sekunden um die Aufgabe zu lösen. Das ist sehr lange, diese Reaktionszeiten weisen in dieser Aufgabe auf fehlende Konzentration hin. Schliessen Sie alle Antwortzeiten aus, welche grösser als 4000ms sind. Auch Reaktionszeiten unter 100ms sind physiologisch unplausibel und werden ausgeschlossen.

# exclude trials with rt > 4000ms
pathrotation <- pathrotation %>%
  filter(rt <= 4000, rt > 100)

Daten visualisieren

Stellen Sie die Reaktionszeiten von drei zufällig ausgewählten Versuchspersonen für Rotationswinkel und Strategie grafisch dar.

set.seed(100)

subjects <- sample(levels(pathrotation$id), 3)
df <- pathrotation %>% 
  filter(id %in% subjects)

# plot response times
df %>% 
  ggplot(aes(rt, fc_angle, color = condition)) +
  geom_point() + 
  scale_color_viridis(discrete=TRUE, option="cividis") +
  facet_grid(id ~ condition, scales = "free_x") +
  theme(legend.position = "none")

Zusatzaufgabe: Verwenden Sie nun einen Violin Plot um die Reaktionszeiten für Winkel und Bedingung darzustellen:

# violin plot
df %>%
  group_by(id, fc_angle, condition) %>%
  ggplot(aes(y = fc_angle, x = rt, fill = condition)) +
  geom_violin(alpha = 0.6) +
  geom_jitter(width = 0.1) +
  scale_fill_viridis(discrete=TRUE, option="cividis") +
  facet_wrap(~ id, scales = "free_x") +
  theme(legend.position = "none")

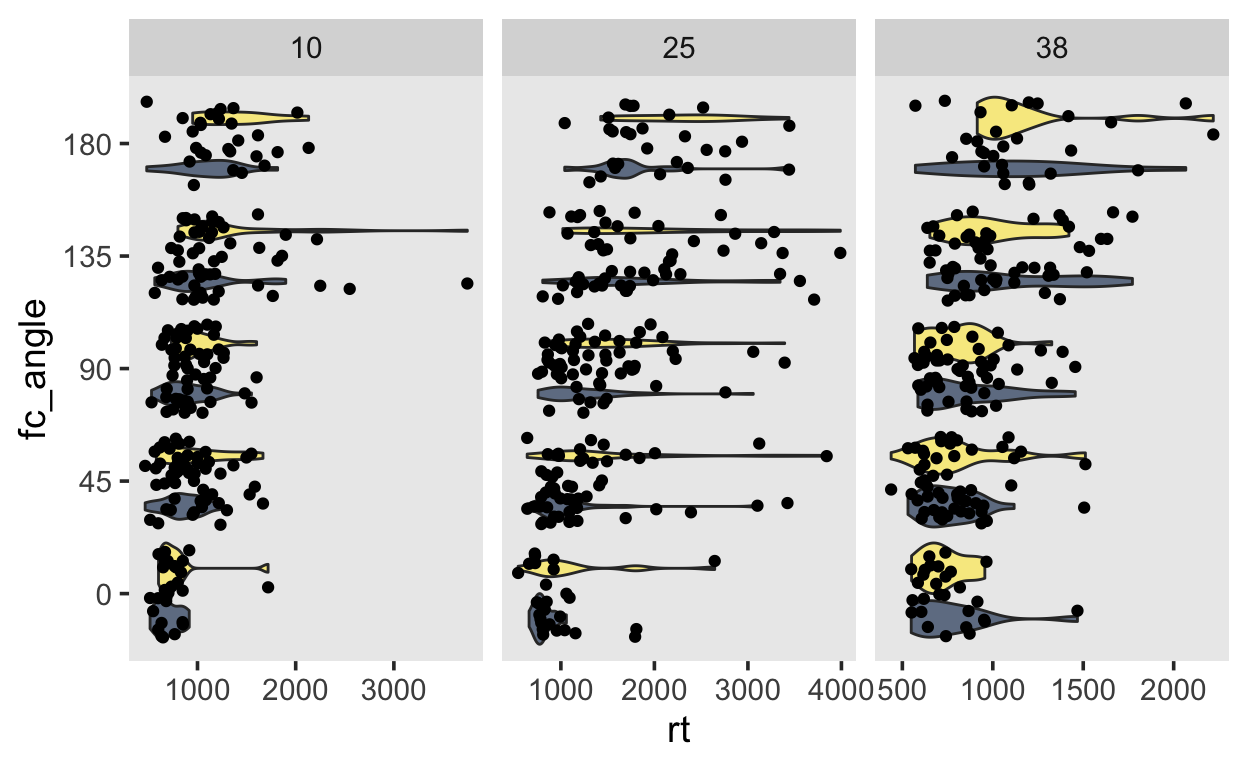
Schauen Sie sich die Grafiken an. Was fällt Ihnen auf?

Was Sie hier sehen hängt natürlich davon ab, welche Personen Sie sich anschauen. Bei den drei dargestellten Versuchspersonen wird ersichtlich, dass die Antwortzeiten mit zunehmendem Rotationswinkeln zunehmen. Die Versuchspersonen hatten zudem eher länger um die Aufgabe mit allozentrischer Strategie zu lösen als mit egozentrischer.

Daten zusammenfassen

Fassen Sie nun die Daten zusammen und stellen Sie sie für jeden Winkel und jede Bedingung mit Mittelwert und Standardfehler dar.

by_id <- pathrotation %>%
  group_by(id, fc_angle, condition) %>% 
  dplyr::summarise(mean = mean(rt),
                   median = median(rt),
                   sd = sd(rt))


# calculate standard error
agg <- Rmisc::summarySEwithin(
  by_id,
  measurevar = "mean",
  withinvars = c("fc_angle", "condition"),
  idvar = "id",
  na.rm = FALSE,
  conf.interval = .95
)

# plot mean and standard errors for angle and condition
agg %>% 
  ggplot(aes(fc_angle, mean)) +
  geom_point(alpha = 0.8) +
  geom_line(aes(group = 1), linetype = 3) +   
  geom_errorbar(aes(ymin = mean-se, ymax = mean+se),
                width = 0.1, size=1, color="black") +
  scale_fill_viridis(discrete=TRUE, option="cividis") +
  facet_wrap( ~ condition) +
  theme(legend.position = "none")

Schauen Sie sich die Plots an. Was wird mit den Punkten dargestellt? Was bedeuten die Balken?

Die Punkte beschreiben den Mittelwert der Antwortzeiten, die Balken den Standardfehler.

Es ist hilfreich sich beim Anschauen von Grafiken in wissenschaftlichen Artikeln immer kurz bewusst zu machen, was die Grafiken wirklich zeigen. Punkte stellen oft Mittelwerte oder Mediane dar. Balken können Standardfehler, Standardabweichungen, Konfidenzintervalle, Credible Intervals, u.v.m. darstellen. In der Übung haben viele fälschlicherweise angenommen, dass diese Balken Standardabweichungen sind.

Sie haben nun sowohl einen Teil der Rohdaten, wie auch die zusammengefassten Daten angeschaut. Was können Sie bezüglich der am Anfang genannten Fragestellungen nun aussagen? (Auch ohne Hypothesentests können Sie mit diesen Grafiken einigermassen sicher sein, ob die Personen die Aufgabe verstanden und gelöst haben oder ob Sie den Task nicht verwenden können.)

Fragestellung 1: Erhöhen sich die Antwortzeiten mit zunehmendem Rotationswinkel?

Sehen Sie in den Daten den erwarteten Rotationseffekt, also dass die Versuchspersonen länger brauchen, wenn sie weiter rotieren müssen (bei grössenen Winkeln)?

Ja, der Rotationseffekt ist sichtbar. Er ist nicht monoton, also stetig (oder linear) sondern ist unterschiedlich abgestuft. Dies ist bei der egozentrischen Rotation zu erwarten, bei der allozentrischen sollte der Anstieg aber monoton sein. Das könnte auf ein Problem im Paradigma hinweisen.

Fragestellung 2: Unterscheiden sich die Antwortzeiten zwischen den beiden Bedingungen in typischer Weise (egozentrisch schneller als allozentrisch)?

Sehen Sie eine Verlangsamung in der Bedingung allozentrisch im Vergleich zu egozentrisch?

Ja, es ist ein Strategieffekt sichtbar. Allerdings ist der Effekt auch bei keiner Rotation (also bei 0 Grad) vorhanden. Das deutet darauf hin, dass die Aufgabe an sich schwieriger ist und nicht die Rotationsstrategie alleine die Verlangsamung generiert.

Explorative Datenanalyse: Shift Function

Vergleichen Sie anhand einer hierarchischen Shift Function die beiden Rotationsbedinungen (separat) bei den Rotationswinkeln 45 Grad, 90 Grad und 180 Grad.

Berechnen Sie die Shift Functions und stellen Sie den Output grafisch dar. Versuchen Sie, die Grafiken zu interpretieren. Erkennen Sie ein Muster?

shiftfun45 <- pathrotation %>% 
    filter(fc_angle == 45) %>% 
    rogme::hsf_pb(rt ~ condition + id)

p_shiftfun45  <- shiftfun45 %>% 
    rogme::plot_hsf_pb(interv = "ci")

p_shiftfun45

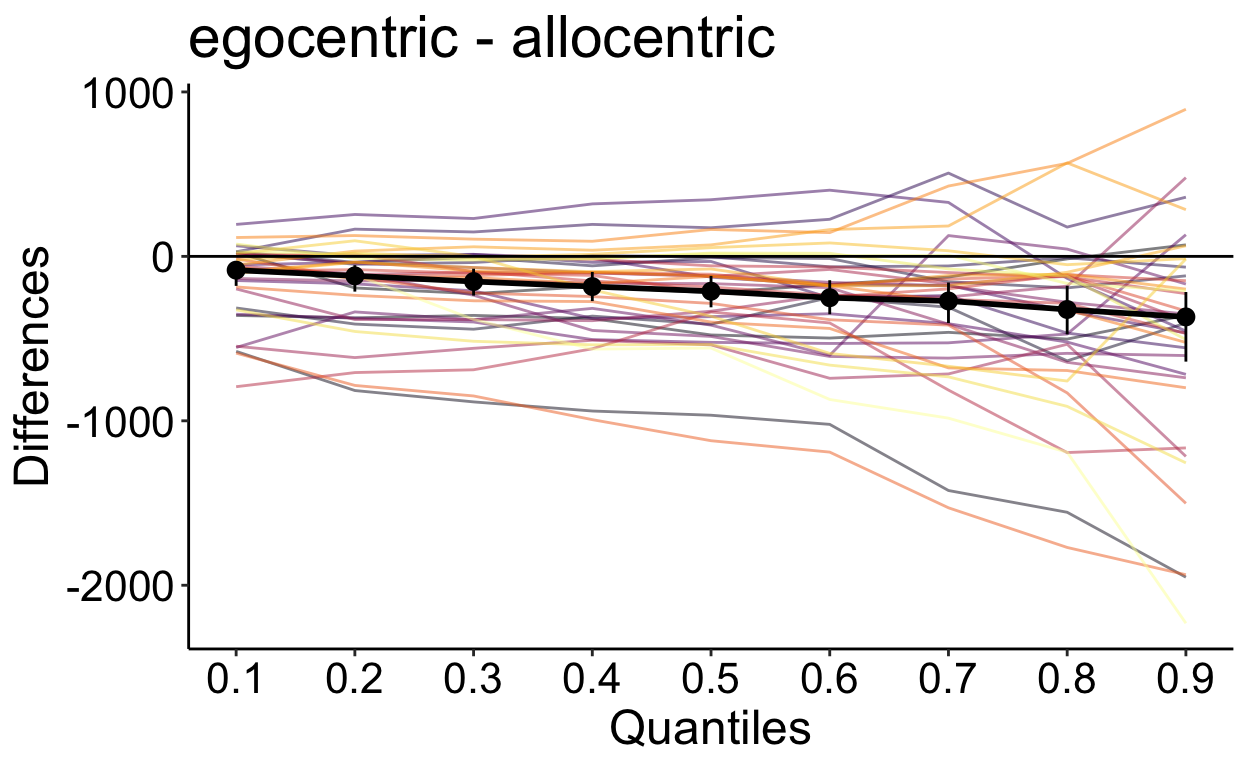
Die schwarzen Punkte verbunden durch die schwarze Linie stellen die mittlere Shift Function dar. In Farbe wurden die Shift Functions aller Personen geplottet. Die Differenz ist bei jedem Dezil negativ und scheint steig grösser zu werden. Bei keinem Dezil ist die Null im Konfidenzinterval enthalten. Wir können nach dieser Methode also davon ausgehen, dass die erste Bedingung (egozentrisch) insgesamt (bei schnellen und langsameren Reaktionszeiten) kürzere Reaktionszeiten als die zweite Bedingung (allozentrisch) hat. Die Differenz wird konstant grösser mit zunehmender Antwortzeit. Ab dem 7. Dezil ist ausserdem zu sehen, dass die Differenz grösser wird. Das könnte darauf hinweisen, dass in der zweiten Bedingung die Personen nicht nur insgesamt langsamer sind, sondern auch variabler. Dieser Effekt gilt jedoch nicht bei allen Personen.

shiftfun90 <- pathrotation %>% 
    filter(fc_angle == 90) %>% 
    rogme::hsf_pb(rt ~ condition + id)

p_shiftfun90  <- shiftfun90 %>% 
    rogme::plot_hsf_pb(interv = "ci")

p_shiftfun90

Hier sieht es ähnlich aus wie beim ersten Plot, nur dass die Differenz über die Dezile hinweg konstanter bleibt.

shiftfun180 <- pathrotation %>% 
    filter(fc_angle == 180) %>% 
    rogme::hsf_pb(rt ~ condition + id)

p_shiftfun180  <- shiftfun180 %>% 
    rogme::plot_hsf_pb(interv = "ci")

p_shiftfun180

Hier scheint die Differenz noch konstanter zu werden, wenn man die mittlere Shift Function betracheten. Die individuellen Abweichungen hingegen werden grösser.

Fazit

Das Ziel der Datenerhebung war es, das Stimulusmaterial zu validieren. Wir haben angeschaut, ob wir den typischen Winkeleffekt finden und ob sich die Strategien wie erwartet unterscheiden.

Wie würden Sie sich aufgrund der Daten entscheiden, verwenden Sie das Stimulusmaterial in ihrer fMRI Studie oder suchen Sie eine andere Lösung?

Für die Planung eines fMRI Experimentes haben wir folgende Erkenntnisse gewonnen:

Feldman, Jason S., and Cynthia Huang-Pollock. 2020. “A New Spin on Spatial Cognition in ADHD: A Diffusion Model Decomposition of Mental Rotation.” Journal of the International Neuropsychological Society, 1–12. https://doi.org/10.1017/S1355617720001198.
Grabherr, Luzia, Cyril Cuffel, Jean-Philippe Guyot, and Fred W. Mast. 2011. “Mental Transformation Abilities in Patients with Unilateral and Bilateral Vestibular Loss.” Experimental Brain Research 209 (2): 205–14. https://doi.org/10.1007/s00221-011-2535-0.
Tomasino, Barbara, and Michele Gremese. 2016. “Effects of Stimulus Type and Strategy on Mental Rotation Network: An Activation Likelihood Estimation Meta-Analysis.” Frontiers in Human Neuroscience 9. https://doi.org/10.3389/fnhum.2015.00693.

References

Corrections

If you see mistakes or want to suggest changes, please create an issue on the source repository.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY 4.0. Source code is available at https://github.com/kogpsy/neuroscicomplab, unless otherwise noted. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".

Citation

For attribution, please cite this work as

Wyssen (2021, June 21). neuroscicomplab: Übung 6. Retrieved from https://kogpsy.github.io/neuroscicomplab/solution-6.html

BibTeX citation

@misc{wyssen2021übung,
  author = {Wyssen, Gerda},
  title = {neuroscicomplab: Übung 6},
  url = {https://kogpsy.github.io/neuroscicomplab/solution-6.html},
  year = {2021}
}

© Copyright 2021 Andrew Ellis

Software licensed under the Creative Commons Zero v4.0 Universal.