Übung 2: Lösung

Parameterschätzung, Posterior zusammenfassen, und lineare Modelle.

true
2021-06-22

Bemerkungen

Aufgabe 1

In der ersten Aufgabe untersuchen Sie einen Datensatz einer Studie, bei der die Arbeitsgedächtnisleitung mittels eines N-Back Tasks bei \(21\) Kindern mit einer ADHS Diagnose untersucht wurde. Gleichzeitig wurde derselbe Task mit einer Kontrollgruppe (\(n=30\)) durchgeführt. Die behavioralen Resultate wurde parallel zu einer fMRI Untersuchung erhoben, damit im Antwortverhalten der Kinder ein Unterschied zur Kontrollgruppe gezeigt werden konnte.

Bei einem N-Back Test wird den Versuchspersonen eine Serie von Stimuli dargeboten (z.B. Buchstaben), und man muss mit einem Tastendruck reagieren, wenn der aktuelle Stimulus gleich dem N-letzten Stimulus war.

Hier sehen Sie ein Beispiel für einen 3-Back Test. Bei den gelb markierten Buchstaben muss die Versuchsperson reagieren.


T A A F A G H R Y Z R V D …

Bei diesem Task untersuchen wir die Reaktionszeiten der Versuchspersonen bei korrekten Antworten. Im Datensatz sind die gemittelten Reaktionszeiten in Sekunden der Kinder in der ADHD und der Control Gruppe.

Daten vorbereiten

Wir laden die Daten:

library(tidyverse)

nback1 <- read_csv("https://raw.githubusercontent.com/kogpsy/neuroscicomplab/main/data/adhd-nback.csv")

Bevor man anfängt, ist es immer eine gute Idee, einen Blick auf die Daten zu werfen.

glimpse(nback1)

Rows: 51
Columns: 2
$ rt    <dbl> 1.0267571, 2.0671470, 1.6728257, 1.0355146, 1.0310874,…
$ group <chr> "adhd", "adhd", "adhd", "adhd", "adhd", "adhd", "adhd"…

Die Gruppierungsvariable group ist ein character Vektor, sollte aber ein Faktor sein.

nback1 <- nback1 %>% 
  mutate(group = as_factor(group))

Nun macht es Sinn, als Referenzkategorie die control group zu bestimmen. Mit fct_relevel() verändern wir die Reihenfolgen der Faktorstufen:

levels(nback1$group)

[1] "adhd"    "control"
nback1 <- nback1 %>% 
  mutate(group = fct_relevel(group, "control"))

control ist nun die erste Stufe, und wir automatisch zur Referenzkategorie, wenn wir die Variable dummy-kodieren.

levels(nback1$group)

[1] "control" "adhd"

Aufgabe 1.1

Berechnen Sie Mittelwerte und SD pro Gruppe.

Zusätzlich berechnen wir gleich noch die Standardfehler, damit wir die Gruppenmittelwerte grafisch darstellen können. Diese Funktion definiere ich hier selber, da sie in base R nicht exisitiert.

se <- function(x) sd(x)/sqrt(length(x))

nback1_summary <- nback1 %>% 
  group_by(group) %>% 
  summarise(mean = mean(rt),
            sd = sd(rt),
            se = se(rt))

nback1_summary

# A tibble: 2 x 4
  group    mean    sd     se
  <fct>   <dbl> <dbl>  <dbl>
1 control  1.15 0.235 0.0430
2 adhd     1.31 0.426 0.0929

Daten visualisieren

Aufgabe 1.2

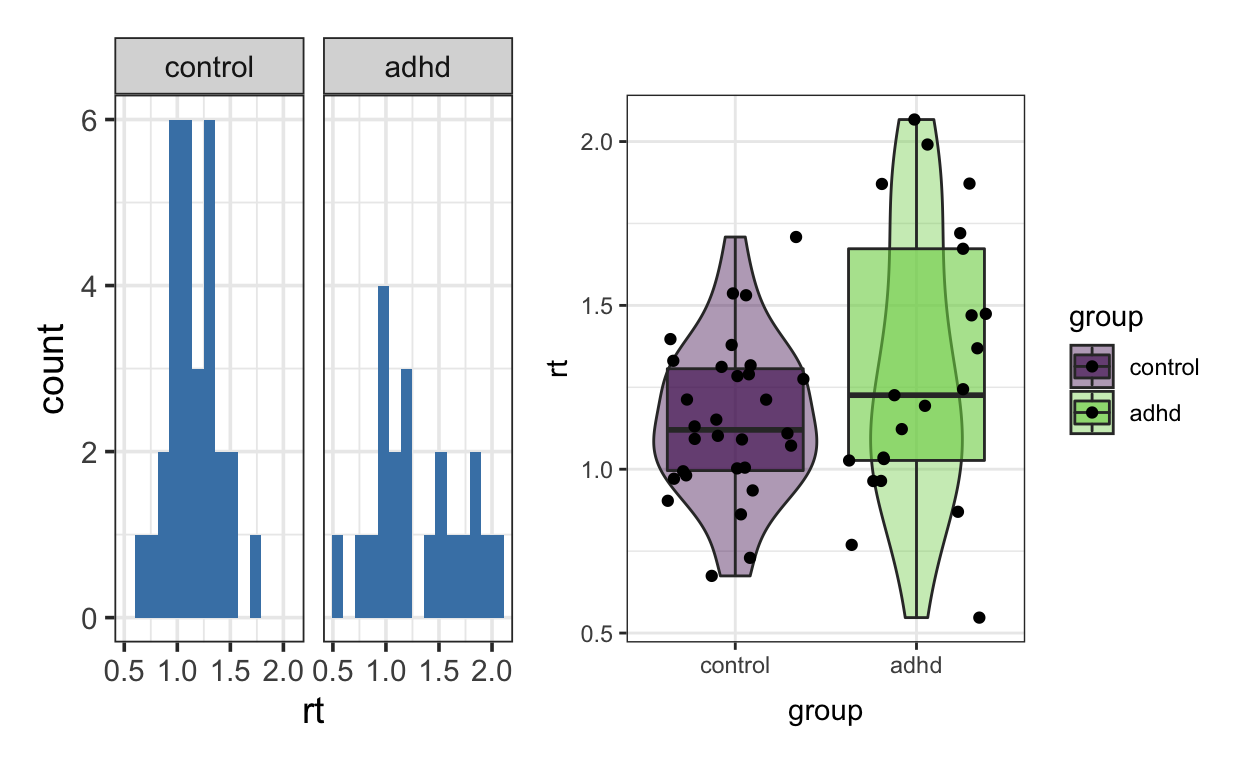
Stellen Sie die Daten mit grafisch dar, zum Beispiel mit Histogrammen, Boxplots oder Violin Plots.

library(patchwork)

p1 <- nback1 %>% 
  ggplot(aes(rt)) +
  geom_histogram(fill = "steelblue", bins = 15) +
  facet_wrap(~group) +
  theme_bw(base_size = 14)

p2 <- nback1 %>% 
  ggplot(aes(group, rt, fill = group)) +
    geom_violin(alpha = 0.4) +
    geom_boxplot(alpha = 0.6) +
  geom_jitter() +
  scale_fill_viridis_d(end = 0.8) +
    theme_bw()

p1 + p2

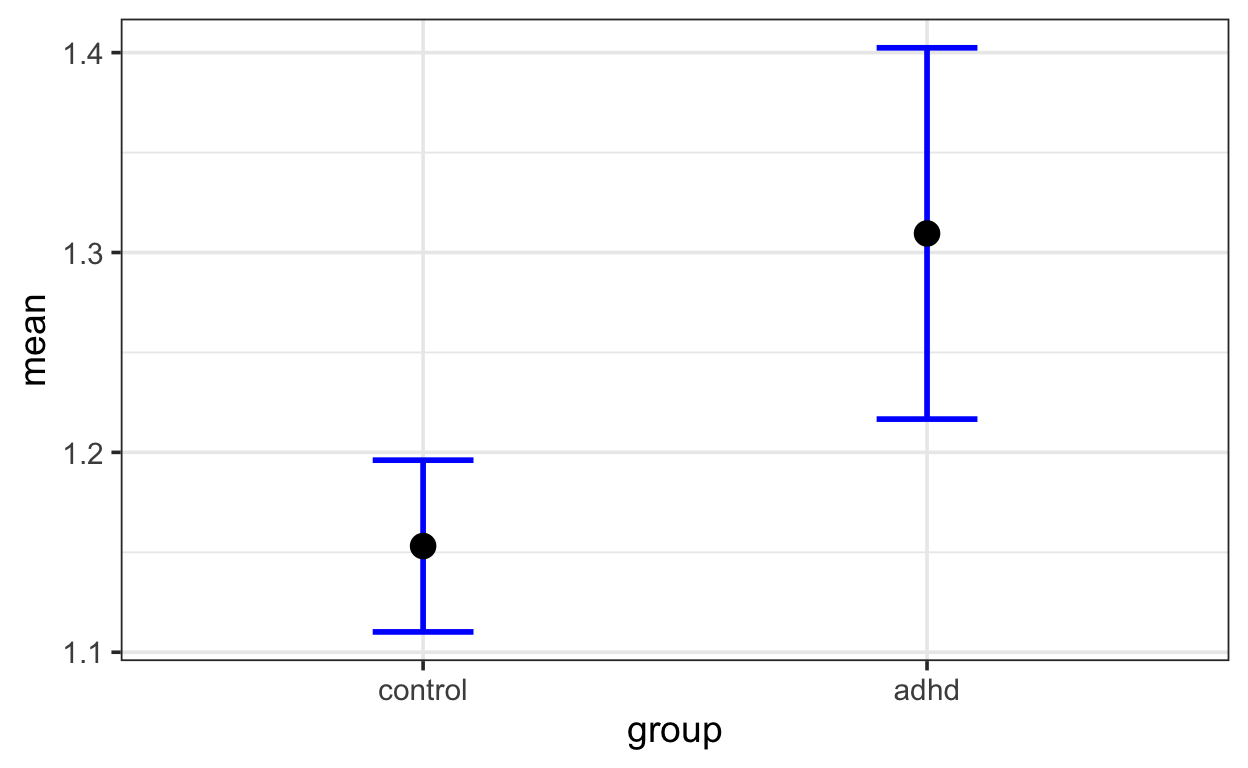
Zusätzlich erstellen wir einen Plot mit eingezeichneten Standardfehlern.

nback1_summary %>% 
  ggplot(aes(group, mean)) +
  geom_errorbar(aes(ymin = mean-se, ymax = mean+se),
                width = 0.2, size=1, color="blue") +
  geom_point(size = 4) +
  theme_bw(base_size = 14)

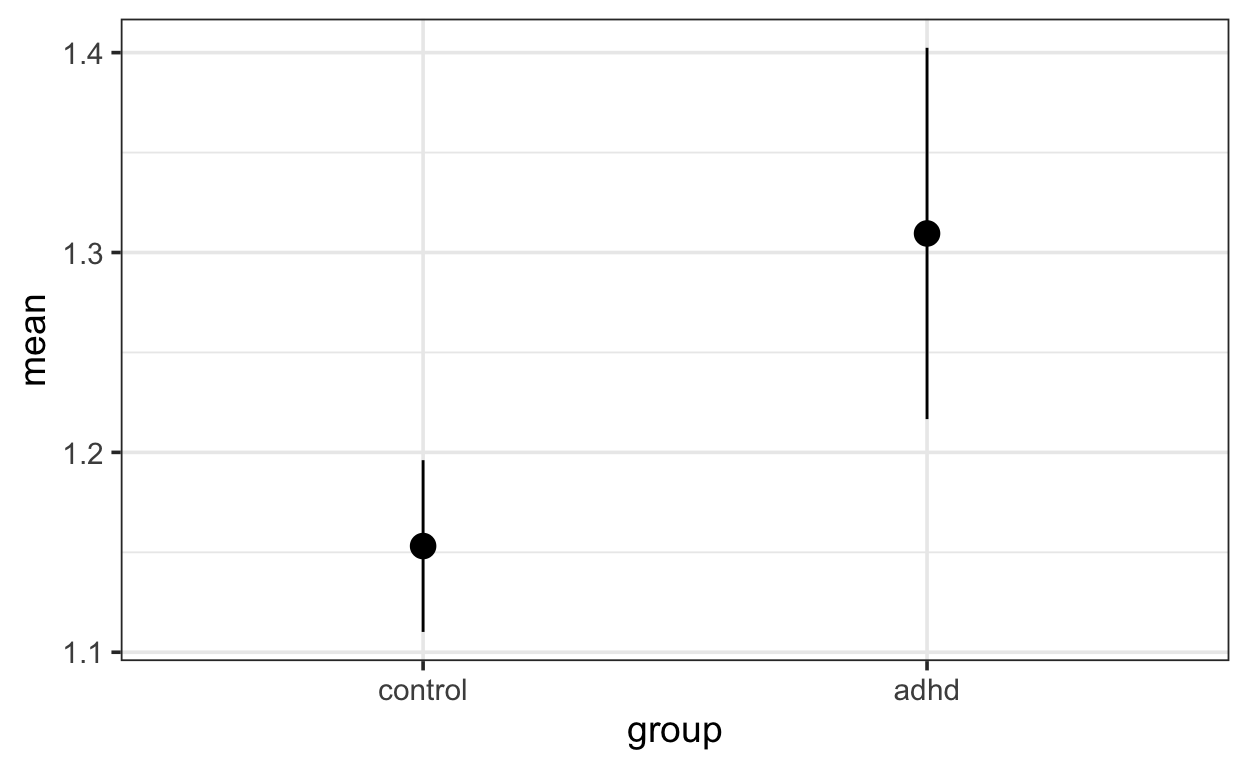
oder

nback1_summary %>% 
  ggplot(aes(group, mean)) +
  geom_linerange(aes(ymin = mean-se, ymax = mean+se)) +
  geom_point(size = 4) +
  theme_bw(base_size = 14)

Frequentistische Analyse

Aufgabe 1.3

Mit welcher Methode würden Sie diese Daten analysieren? Beschreiben Sie Ihre Wahl in 1-2 Sätzen und führen Sie einen Test durch. Was können Sie damit aussagen?

Wir können hier annehmen, dass die Kinder in der adhd Gruppe länger brauchen. Dies bedeutet, dass wir eine gerichtete Hypothese testen. Es ist in den meisten Fällen sinnvoll, einen Welch Test durchzuführen. Dies ist auch der Default in R (wenn wir einen t-Test wünschen, müssen wir dies explizit angeben, mit var.eq = TRUE).

t.test(rt ~ group,
       data = nback1,
       alternative = "less")


    Welch Two Sample t-test

data:  rt by group
t = -1.5282, df = 28.57, p-value = 0.06873
alternative hypothesis: true difference in means between group control and group adhd is less than 0
95 percent confidence interval:
       -Inf 0.01757687
sample estimates:
mean in group control    mean in group adhd 
             1.153130              1.309528

Selbst wenn wir einen gerichteten t-Test durchführen, erhalten wir einen p-Wert von 0.0687. Dies bedeutet, dass wir unter Verwendung von \(\alpha = 0.05\) die Nullhypothese nicht ablehnen dürfen. Falls Sie hier ungerichtet getestet haben, haben Sie einen p-Wert von \(0.1375\) erhalten (entspricht dem doppeltem einseitigen p-Wert).

t.test(rt ~ group,
       data = nback1)


    Welch Two Sample t-test

data:  rt by group
t = -1.5282, df = 28.57, p-value = 0.1375
alternative hypothesis: true difference in means between group control and group adhd is not equal to 0
95 percent confidence interval:
 -0.36584395  0.05304754
sample estimates:
mean in group control    mean in group adhd 
             1.153130              1.309528

In beiden Fällen können wir also die Nullhypothese nicht ablehnen. Diese sagt aus, dass die beiden Gruppen in Bezug auf die Teststatistik nicht unterscheiden, d.h. in Bezug auf dem Gruppenmittelwert. Mehr können wir mit diesem t-Test nicht aussagen. Dies ist etwas unglücklich, da unser Ziel wahrscheinlich war, einen Unterschied mit funktioneller Bildgebung zu untersuchen.

Selbstverständlich hätten wir grössere Stichproben nehmen sollen; dies ist aber in fMRI Studien nicht immer möglich, und führt dazu, dass viele Studien under-powered sind.

Bayesianische Analyse

Wir wollen nun die beiden Gruppenmittelwerte Bayesianisch schätzen. Sie haben zwei Möglichkeiten kennengelernt, die Formel zu spezifieren.

Aufgabe 1.4

Entscheiden Sie sich für eine der beiden, und schätzen sie die Mittelwerte mit brms. Schauen Sie sich vorher mit der Funktion get_prior die Default Prior Verteilungen an. Wenn sie wollen, können Sie anstelle der Defaults eigene Priors spezifieren. Falls Sie das tun, begründen Sie kurz Ihre Wahl.

Mit den zwei Möglichkeiten sind die folgenden gemeint:

rt ~ 1 + group

und

rt ~ 0 + group

Die beiden Formeln können wir so verstehen:

rt ~ 1 + group

wird zu

rt ~ b0 * 1 + b_group * group

Wir haben also einen Achsenabschnitt (Intercept) b0 und einen Regressionskoeffizienten b_group. Wenn die Variable group dummy kodiert ist, dann ist b_group der Unterschied zwischen den Gruppen.

Die Formel

rt ~ 0 + group

wird zu

rt ~ b0 * 0 + b_groupcontrol * groupcontrol + b_groupadhd * groupadhd

Hier haben wir keinen Achsenabschnitt, so dass wir beide Indikatorvariablen verwenden können. Die beiden Koeffizienten repräsentieren deshalb die beiden Gruppenmittelwerte.

Etwas, das oft falsch gemacht wurde: Mit der Formel rt ~ 1 wird ein Achsenabschnitt geschätzt. Dies wäre das Nullmodell, denn hier wird die Gruppierungsvariable weggelassen, und wir schätzen den Gesamtmittelwert.

Nun schauen wir uns für beide Möglichkeiten die Priors an. Wenn wir rt ~ 1 + group oder einfach rt ~ group verwenden, dann erhalten wir einen student_t(3, 1.2, 2.5) Prior für den Intercept, und einen flachen Prior für den Unterschied.

library(brms)

get_prior(rt ~ 1 + group,
          data = nback1)

                  prior     class      coef group resp dpar nlpar
                 (flat)         b                                
                 (flat)         b groupadhd                      
 student_t(3, 1.2, 2.5) Intercept                                
   student_t(3, 0, 2.5)     sigma                                
 bound       source
            default
       (vectorized)
            default
            default

Wenn wir den Intercept weglassen, erhalten wir für beide Gruppen flache Priors:

get_prior(rt ~ 0 + group,
          data = nback1)

                prior class         coef group resp dpar nlpar bound
               (flat)     b                                         
               (flat)     b    groupadhd                            
               (flat)     b groupcontrol                            
 student_t(3, 0, 2.5) sigma                                         
       source
      default
 (vectorized)
 (vectorized)
      default

Wenn wir uns hier für die ersten Variante entscheiden, können wir eine besseren Prior spezifieren. Z.B. könnten wir a priori 95% sicher sein, dass der Gruppenunterschied zwischen -10 und +10 liegt. Dies können wir mit dem Prior normal(0, 5) ausdrücken.

priors <- prior(normal(0, 5), class = b)

Aufgabe 1.5

Schätzen Sie nun die Parameter Ihres Modells.

m1 <- brm(rt ~ group,
          prior = priors,
          data = nback1,
          file = "nback1")

summary(m1)

 Family: gaussian 
  Links: mu = identity; sigma = identity 
Formula: rt ~ group 
   Data: nback1 (Number of observations: 51) 
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup samples = 4000

Population-Level Effects: 
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept     1.15      0.06     1.03     1.28 1.00     3165     2552
groupadhd     0.16      0.10    -0.03     0.34 1.00     3484     2506

Family Specific Parameters: 
      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma     0.34      0.04     0.28     0.41 1.00     2763     2124

Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
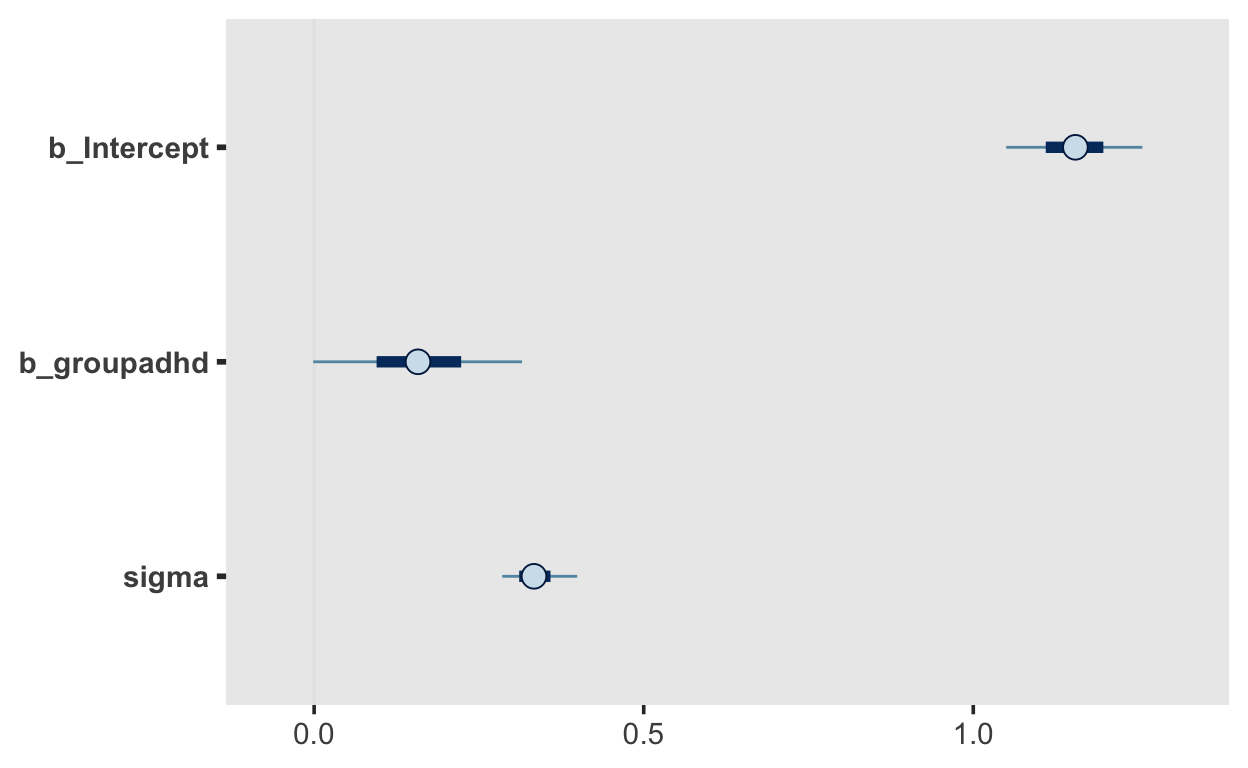
scale reduction factor on split chains (at convergence, Rhat = 1).

Es werden hier 3 Parameter geschätzt: Intercept, groupadhd und sigma. Letzter ist die Standardabweichung der Residuuen. Alle 3 Parameter haben ein Rhat von 1.00. Wir sollten darauf achten, dass Rhat nicht >1.05 ist. Dies würde bedeuten, dass die 4 Chains, welche unabhängig voneinander sind, nicht dieselbe Posterior Verteilung geschätzt haben, was natürlich nicht das ist, was wir wollen.

Wir haben hier nur ein sigma geschätzt, was bedeutet, dass wir für beide Gruppen dieselbe Standardabweichung annehmen. Diese Annahme ist nicht nötig, wir könnten genausogut auch 2 Standardabweichungen schätzen. Dies würde so aussehen:

m1b <- brm(bf(rt ~ group, sigma ~ group),
          prior = priors,
          data = nback1,
          file = "nback1-b")

In diesem Modell sagen wir sowohl den Mittelwert als auch die Standardabweichung anhand der Gruppenzugehörigkeit vorher. Das heisst, dass wir hier relitiv flexibel unser Modell spezifizieren können, und zwar so dass wir die interessierenden Parameter besser schätzen können. Dies soll an dieser Stelle einfach mal die Flexibilität von Bayesianischer Inferenz illustrieren — dieses Vorgehen wäre mit frequentistischer Statistik nicht möglich. Wir bräuchten ein eigens dafür entwickeltes Verfahren, und müssten hoffen, dass jemand ein R Package dafür schreibt.

Alle Parameter, welche wir in unserem Modell spezifiziert haben, erscheinen nun auch im Ouput.

Die beiden Parameter Intercept, groupadhd interessieren uns hier besonders. Der Intercept ist der erwartete Wert der Kontrollgruppe, während groupadhd der Unterschied zwischen den Gruppen ist.

Optionale Aufgabe: fassen Sie die Posterior Verteilung des/der relevanten Parameter(s) mit Hilfe der Funtion mean_qi() im tidybayes Packages zusammen.

library(tidybayes)

samples1 <- m1 %>% 
  posterior_samples() %>% 
  transmute(Differenz = b_groupadhd) 

samples1 %>% 
  mean_qi()

  Differenz      .lower    .upper .width .point .interval
1 0.1579944 -0.03237111 0.3435227   0.95   mean        qi

Grafische Darstellung

Anstatt sich nur eine Tabelle anzuschauen, ist es hilfreich, die Verteilungen grafisch darzustellen.

Aufgabe 1.6

Stellen Sie die Posterior Verteilung(en) grafisch dar. Sie können dies entweder mit der Funktion mcmc_plots() im brms Package, oder (optional) mit dem tidybayes Package machen. Eine Anleitung für das tidybayes Package finden Sie im 3. Kapitel des Skripts.

Mit der Funktion mcmc_plot() können wir eigentlich alles darstellen. Entweder alle Koeffizienten, die beiden Regressionkoeffizienten, oder nur den Unterschiedskoeffizienten.

m1 %>% 
  mcmc_plot()


m1 %>% 
  mcmc_plot("b")

Wir können auch die Breite des Credible Intervals ändern, so dass wir die 50% und 95% Credible Intervals erhalten.

m1 %>% 
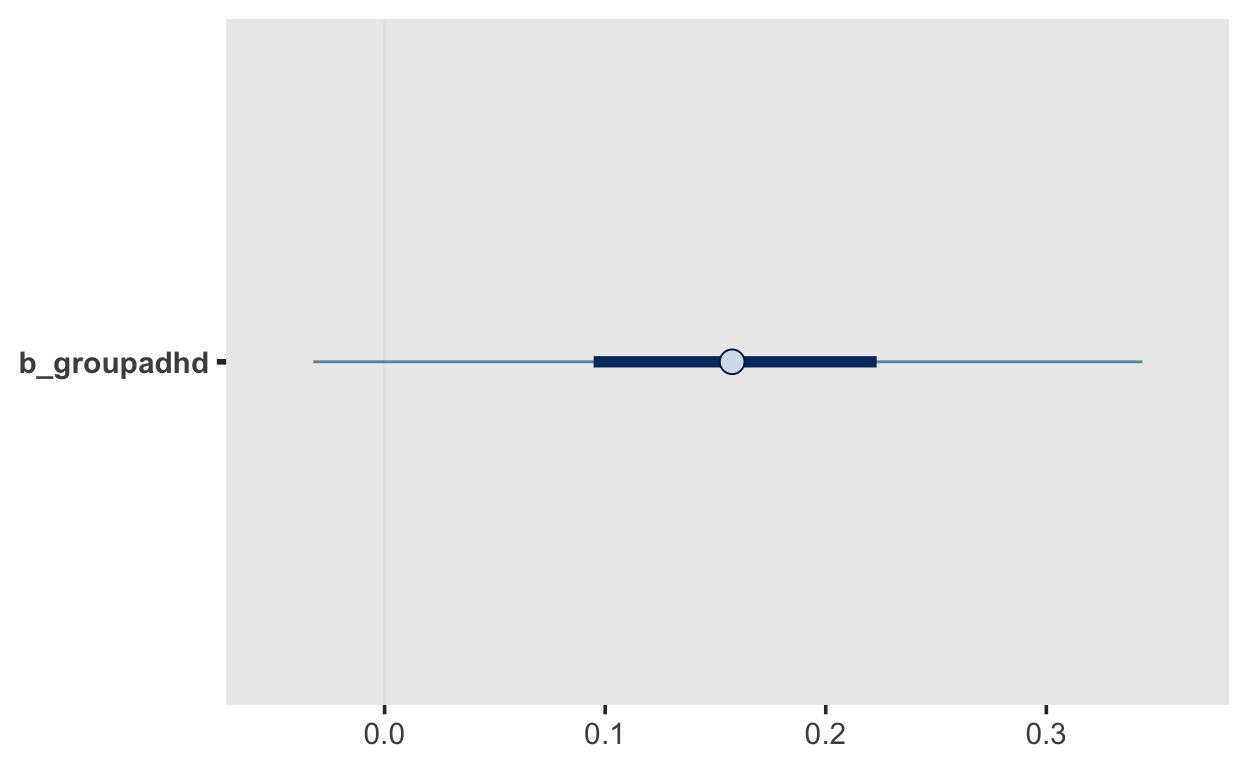
  mcmc_plot("b_group", prob = 0.5, prob_outer = 0.95)

Diskussion

Aufgabe 1.7

Diese Frage ist nicht ganz einfach. Mit der Frage “Welche Aussagen dürfen Sie nicht machen?” ist natürlich gemeint, dass wir hier bisher noch keine Hypothese getestet haben, oder zumindest nicht explizit. Implizit haben wir hier zwar die Hypothese, dass es einen Unterschied gibt, den wir schätzen können (mehr dazu später). In diesem einen Modell können wir nun aussagen, in welchen Bereich sich die wahrscheinlichen Werte des Unterschieds befinden. Laut dem Output sind wir 95% sicher, dass der Gruppenunterschied zwischen \(-0.02\) und \(0.34\) liegt. Der Unterschied ist am ehesten > 0. Wir können sogar genau quantifizieren, wie sicher wir uns dessen sind.

Wir berechnen einfach den Anteil der Samples, für welche die Differenz > 0 ist.

samples1 %>% 
  count(Differenz > 0) %>% 
  mutate(probability = n / sum(n))

  Differenz > 0    n probability
1         FALSE  204       0.051
2          TRUE 3796       0.949

Dies bedeutet, dass wir uns uns 95.5% sicher, dass die Differenz positiv ist. Da wir aber das Nullmodell nicht geschätzt haben, können wir an dieser Stelle keinen Modellvergleich machen. Das Nullmodell ist nämlich dasjenige Modell, in dem die Differenz auf den Wert 0 fixiert wird, d.h. nicht geschätzt wird. Nur wenn wir die beiden Modelle in Bezug auf ihre prädiktiven Fähigkeiten vergleichen, können wir eine Hypothese testen. Etwas, das wir aber hier nicht tun müssen, ist eine binäre Entscheidung zu treffen (Nullhypothese ablehen oder nicht). Diese Entscheidung braucht nämlich eine sogenannte Nutzenfunktion, und diese ist in der frequentistischen Statistik die 5% Fehlerwahrscheinlichkeit. Dies bedeutet, dass Sie bei einem NHST bereit sind, im Schnitt bei jeder 20. Entscheidung einen Fehler zu machen. Dies ist aber nicht zwingend notwendig, da wir auch einfach Evidenz für oder gegen Hypothesen quantifizieren können. Dafür brauchen wir aber z.B. Bayes Factors.

Ganz entscheidend ist hier: wir schätzen hier bedingt auf die Daten die wahrscheinlichen Werte für die Differenz der beiden Gruppen, welche diese Daten generiert haben könnten. In einem NHST wird mehr gemacht. Dort nehmen wir eine Stichprobe, fassen diese anhand von “summary statistics” zusammmen, und schauen uns dann die theoretische Verteilung der summary statistics (in diesem Fall die Mittelwertsdifferenz) unter der Nullhypothese an. Diese Prozedur erlaubt uns auszusagen, wie wahrscheinlich es ist, eine solch grosse Differenz zu erhalten (p-Wert). Anhand dieses p-Wertes kann eine Entscheidung getroffen werden—ob dies eine gute Idee ist, sei dahingestellt. Auf jeden Fall ist die Grenze \(\alpha = 0.05\) willkürlich gewählt, und bedeutet einfach, dass wir bei jeder 20. Entscheidung einen Fehler in Kauf nehmen.

Es gibt einen Trick, wie wir einfach zu dem Anteil der Posterior Samples kommen, welcher über einem Schwellenwert liegt. Wir können einfach die Funktion hypothesis() benutzen!

Diese verwenden wir so: wir spezifieren unsere “Hypothese” (in Anführungszeichen, weil der Begriff hier nicht ganz richtig verwendet wird) so: "groupadhd > 0", und erhalten im Oouput ein Evidence Ratio (Evid.Ratio). In diesem Fall beträgt dieses 21.22, was genau der Wahrscheinlichkeit von "groupadhd > 0" geteilt durch die Gegenwahrscheinlichkeit "groupadhd <= 0" entspricht. Sie erhalten auch die Post.Prob; dies ist P("groupadhd > 0").

m1 %>% 
  hypothesis("groupadhd > 0")

Hypothesis Tests for class b:
       Hypothesis Estimate Est.Error CI.Lower CI.Upper Evid.Ratio
1 (groupadhd) > 0     0.16       0.1        0     0.32      18.61
  Post.Prob Star
1      0.95     
---
'CI': 90%-CI for one-sided and 95%-CI for two-sided hypotheses.
'*': For one-sided hypotheses, the posterior probability exceeds 95%;
for two-sided hypotheses, the value tested against lies outside the 95%-CI.
Posterior probabilities of point hypotheses assume equal prior probabilities.

Aufgabe 2

In der zweiten Aufgabe untersuchen wir einen Datensatz einer Studie, bei der die Arbeitsgedächtnisleitung mittels eines N-Back Tasks bei 20 gesunden Erwachsenen unter verschiedenen Cognitive Loads untersucht wurde. Ziel dieser Studie war es, die Auswirkung von Cognitive Load auf den Präfrontalen Cortex mittels fMRI zu untersuchen. Wir erwarten, dass bei höherem Cognitive Load die Versuchspersonen länger brauchen, um beim N-Back Task eine korrekte Antwort zu geben.

Der letzte Satz lässt darauf schliessen, dass wir eine gerichtete Hypothese haben.

Daten vorbereiten

Wir laden die Daten:

library(tidyverse)
library(rmarkdown)

nback2 <- read_csv("https://raw.githubusercontent.com/kogpsy/neuroscicomplab/main/data/cognitive-load-nback.csv") %>% 
  mutate(across(-rt, as_factor))
nback2 %>% paged_table()

Wir haben 20 Personen

nback2 %>% 
  summarize(n_subjects = n_distinct(id))

# A tibble: 1 x 1
  n_subjects
       <int>
1         20

mit 60 Trials pro Person pro Bedingung. Für jeden Trial haben wir die Reaktionszeit in Millisekunden.

nback2 %>% 
  group_by(id, load) %>% 
  count() %>% 
  rmarkdown::paged_table()

Daten zusammenfassen

Da die Standardfehler Funktion in R nicht existiert, schreiben wir selber eine (haben wir weiter oben schon gemacht):

se <- function(x) sd(x)/sqrt(length(x))

Aufgabe 2.1

Fassen Sie die Daten mit Mittelwert, Standardabweichung und Standardfehler pro Person pro Bedingung zusammen.

Mit diesem Code kann ich gleichzeitig 3 Funktionen anwenden (ist effizienter):

nback2 %>% 
  group_by(id, load) %>% 
  summarise(mean = mean(rt),
            sd = sd(rt), 
            se = se(rt))

# A tibble: 40 x 5
# Groups:   id [20]
   id    load   mean    sd    se
   <fct> <fct> <dbl> <dbl> <dbl>
 1 1     hi     933.  28.0  3.62
 2 1     lo     877.  26.8  3.46
 3 2     hi     842.  25.7  3.31
 4 2     lo     789.  24.3  3.14
 5 3     hi     936.  30.8  3.97
 6 3     lo     887.  27.0  3.48
 7 4     hi    1030.  20.9  2.70
 8 4     lo     976.  26.8  3.46
 9 5     hi     834.  23.1  2.99
10 5     lo     796.  24.7  3.19
# … with 30 more rows

Wir erhalten so die mittlere Reaktionszeit für jede Person in jeder Bedingung, plus die SD und die Standardfehler.

Aufgabe 2.2

Sie haben die Kennzahlen für jede Person berechnet. Meistens wollen wir aber nicht nur die Effekte der experimentellen Manipulationen für Individuen, sondern für die ganze Gruppe.

Berechnen Sie die mittlere RT für die beiden Bedingungen, aggregiert über Personen. Wie würden Sie vorgehen? Überlegen Sie sich, was die Vor- und Nachteile eines solches Vorgehens sind, und beschreiben Sie sie kurz.

Meistens wollen wir eine generalisierte Aussage machen können—eine Manipulation soll nicht nur bei einzelnen Individuen einen Effekt haben, sondern in einer Population von gleichen Individuen. Wir haben hier nur den mittlere RT aggregiert über Personen berechnet. Für die Berechnung der Standardfehler müssen wir berücksichtigen, dass die Manipulation des cognitive loads eine “within” Manipulation ist. Dies können wir mit der Funktion summarySEwithin() aus dem Rmisc Package machen.

agg <- Rmisc::summarySEwithin(nback2,
                        measurevar = "rt",
                        withinvars = "load",
                        idvar = "id",
                        na.rm = FALSE,
                        conf.interval = 0.95)
agg

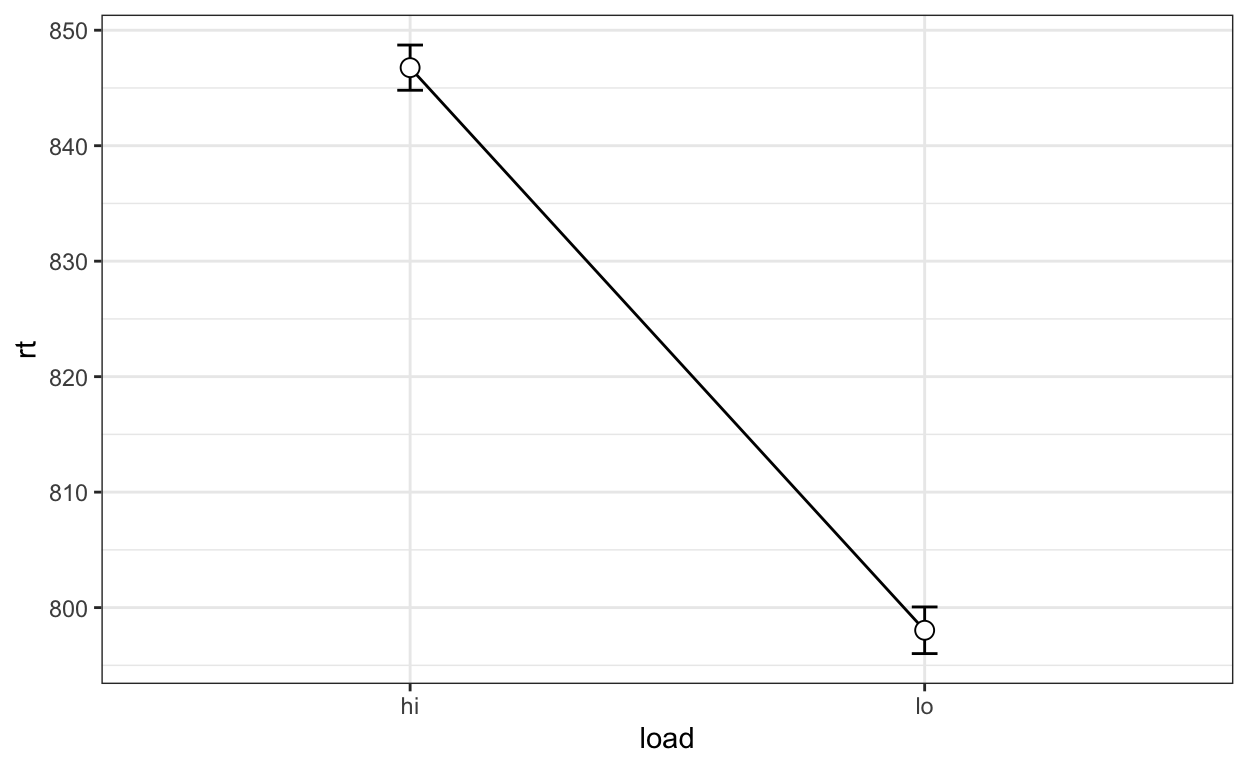
  load    N       rt       sd        se       ci
1   hi 1200 846.7592 34.56937 0.9979319 1.957887
2   lo 1200 798.0375 35.67373 1.0298120 2.020434

Selbst wenn wir berücksichtigen, dass die load Bedingung within manipuliert wurde, so haben wir trotzdem noch foglendes Problem: die unsicherheit, die wir bei der Aggregation der RTs der einzelnen Personen haben, wrd einfach ignoriert—wir ersetzen ja die einzelnen Messwerte einfach durch den personenspezifischen Mittelwert für die beiden Bedingungen. Das heisst, anstelle der Verteilung von RTs, welche ziemlich variieren können, nehmen wir einfach den Mittelwert, und hoffen, dass dieser die RTs ausreichend gut zusammenfasst. Dies ist bei RTs leider oft nicht der Fall, da sie eine ausgeprägt Rechtsschiefe aufweisen können.

Diese Aggregation führt dazu, dass wir uns viel zu sicher sind, und die über die Personen aggregegierten Mittelwerte uns ein falsches Gefühl von Sicherheit vermitteln, in dem Sinne, dass sie viel weniger präzise sind, als wir glauben.

Eine sehr gute Methode, um damit umzugehen, ist die Verwendung von Multilevel Modellen—wir bevorzugen hier den Ansatz, die beide Ebenen (Level 1 und Level 2) gleichzeitig zu schätzen, so dass die Unsichersheit nicht einfach weggeworfen wird.

Daten visualisieren

Auch hier ist es sinnvoll, die Daten zuerst grafisch darzustellen.

Aufgabe 2.3

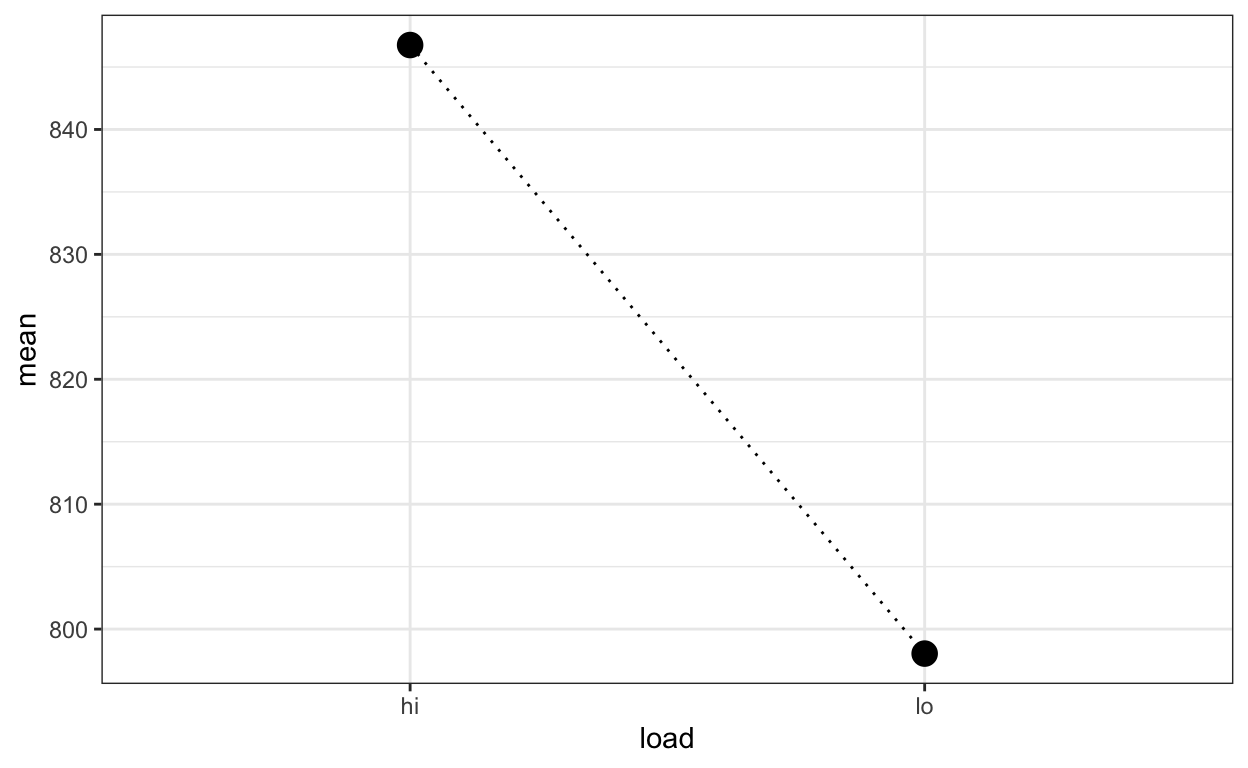
Stellen Sie die mittleren RTs für jede Bedingung aggregiert über Personen grafisch dar.

aggregated %>% 
  ggplot(aes(load, mean)) +
  geom_line(aes(group = 1), linetype = 3) +
  geom_point(size = 4) +
  theme_bw()


agg %>%
    ggplot(aes(x = load, y = rt, group = 1)) +
    geom_line() +
    geom_errorbar(width =.05, aes(ymin = rt-ci, ymax = rt+ci)) +
    geom_point(shape = 21, size = 3, fill = "white") + 
    theme_bw()

Frequentistische Analyse

Aufgabe 2.4

Überlegen Sie sich, wie Sie diesen Datensatz frequentistisch analysieren könnten. Beschreiben Sie in 1-2 Sätzen, was Sie tun würden, und welche Aussagen Sie damit machen könnten.

Die einfachste Möglichkeit ist ein paired-samples t-Test.

t.test(rt ~ load, 
       data = nback2, 
       alternative = "greater",
       paired = TRUE)


    Paired t-test

data:  rt by load
t = 47.772, df = 1199, p-value < 2.2e-16
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
 47.04283      Inf
sample estimates:
mean of the differences 
               48.72167

Dieser zeigt uns an, dass wir eine Mittelwertsdifferenz zwischen den cognitive load Bedingungen von 48.72 haben, und dass diese Differenz signifikant ist. Das bedeutet genau, dass die Wahrscheinlichkeit, einen t-Wert von 47.772 unter Nullhypotheses zu erhalten klein genug ist, um mit einem Fehlerrisiko von \(\alpha = 0.05\) die Nullhypothese abzulehnen.

Wir könnten hier aber auch ein Multilevel-Modell benutzen:

Es ist sinnvoll, die low cognitive load Bedingung als Referenz zu wählen.

nback2 <-  nback2 %>% 
  mutate(load = fct_relevel(load, "lo"))

library(lme4)
library(lmerTest)

m_mle_1 <- lmer(rt ~ load + (1 | id),
           data = nback2,
           REML = TRUE)

Nun erhalten wir den Parameter loadhi, welcher die Differenz zwischen den Bedingungen repräsentiert, nachdem wir die Messwiederholung innerhalb der Personen berücksichtigt haben.

summary(m_mle_1)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: rt ~ load + (1 | id)
   Data: nback2

REML criterion at convergence: 22382.8

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.5379 -0.6827  0.0229  0.6697  3.9772 

Random effects:
 Groups   Name        Variance Std.Dev.
 id       (Intercept) 7305.3   85.47   
 Residual              621.8   24.94   
Number of obs: 2400, groups:  id, 20

Fixed effects:
            Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)  798.037     19.125   19.027   41.73   <2e-16 ***
loadhi        48.722      1.018 2379.000   47.86   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
       (Intr)
loadhi -0.027

Wir könnten hier auch annehmen, dass die Personen sich auch im Effekt der Bedinungung unterscheiden (random intercept und random slope Modell):

m_mle_2 <- lmer(rt ~ load + (1 + load | id),
           data = nback2,
           REML = TRUE)
summary(m_mle_2)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: rt ~ load + (1 + load | id)
   Data: nback2

REML criterion at convergence: 22382.1

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.5627 -0.6749  0.0220  0.6601  3.9909 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 id       (Intercept) 7354.849 85.760        
          loadhi         4.717  2.172   -0.27
 Residual              620.711 24.914        
Number of obs: 2400, groups:  id, 20

Fixed effects:
            Estimate Std. Error      df t value Pr(>|t|)    
(Intercept)  798.037     19.190  18.999   41.59   <2e-16 ***
loadhi        48.722      1.127  19.001   43.23   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
       (Intr)
loadhi -0.141

Bayesianische Analyse

Wir wollen nun die population-level Effects mit brms schätzen, und zwar die Mittelwerte der beiden Cognitive Load Bedingungen. Dafür benutzen wir die Formel ~ 0 + load. Die population-level Effects entsprechen den Fixed effects im Output von lme4.

Wir erhalten folgende Default Priors:

get_prior(rt ~ 0 + load + (1 | id),
          data = nback2)

                 prior class      coef group resp dpar nlpar bound
                (flat)     b                                      
                (flat)     b    loadhi                            
                (flat)     b    loadlo                            
 student_t(3, 0, 94.1)    sd                                      
 student_t(3, 0, 94.1)    sd              id                      
 student_t(3, 0, 94.1)    sd Intercept    id                      
 student_t(3, 0, 94.1) sigma                                      
       source
      default
 (vectorized)
 (vectorized)
      default
 (vectorized)
 (vectorized)
      default

Die beiden flachen Priors der Parameter loadhi und loadlo wollen wir nun durch eigene Priors ersetzen. Wir nehmen hier einfach Normalverteilungen, mit einem Mittelwert, der dem Gesamtmittelwert entspricht, und einer etwas arbiträr gewählten Standardabweichung von \(10\).

grandmean <- round(mean(nback2$rt), 0)
grandmean

[1] 822

Priors können mit set_prior() oder einfach nur prior() definiert werden.

priors <- set_prior("normal(822, 10)", class = "b")
# oder
priors <- prior(normal(822, 10), class = b)

Wir schätzen das Model nun mit unseren Prior Verteilungen.

m2 <- brm(rt ~ 0 + load + (1 | id),
          prior = priors,
          data = nback2,
          file = "nback2")

Posterior zusammenfassen und Grafische Darstellung

Aufgabe 2.5

Überprüfen Sie, ob die Rhat Werte in Ordnung sind. Falls ja, fassen Sie die Posterior Verteilung der wichtigen Parameter zusammen. Stellen Sie die Posterior Verteilungen der beiden Bedingungsparameter grafisch dar, z.B. mit mcmc_plot().

summary(m2)

 Family: gaussian 
  Links: mu = identity; sigma = identity 
Formula: rt ~ 0 + load + (1 | id) 
   Data: nback2 (Number of observations: 2400) 
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup samples = 4000

Group-Level Effects: 
~id (Number of levels: 20) 
              Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS
sd(Intercept)    86.88     13.89    63.37   118.19 1.01      306
              Tail_ESS
sd(Intercept)      601

Population-Level Effects: 
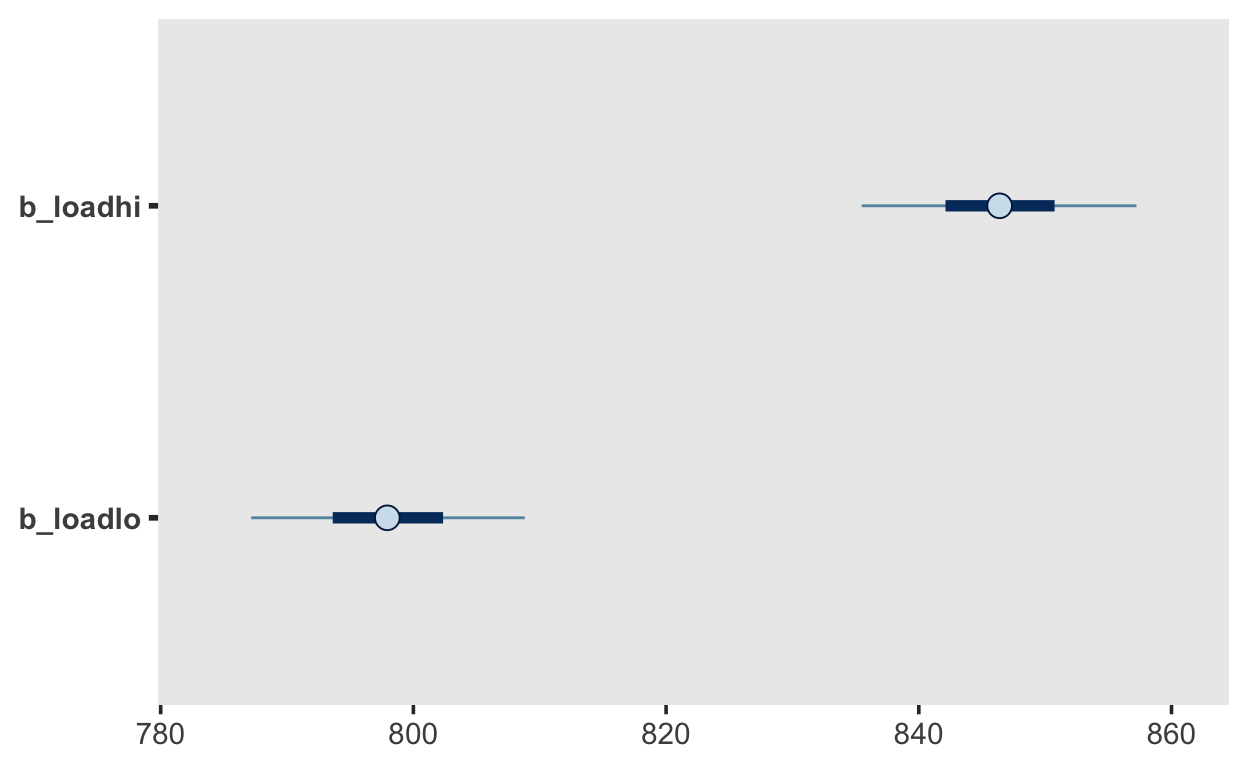
       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
loadhi   846.40      6.58   833.08   859.34 1.01      527      697
loadlo   797.94      6.58   784.84   810.94 1.01      522      697

Family Specific Parameters: 
      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma    24.96      0.36    24.29    25.70 1.00     1562     1440

Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Die Rhat Werte sind in Ordnung. Wir erhalten die Parameter loadhi, loadlo, sigma und sd(Intercept). sd(Intercept) ist die Standardabweichung der personenspezifischen Abweichungen von Achsenabschnitt. Das ist vielleicht etwas verwirrend, denn wir haben hier keinen Achsenabschnitt. Eigentlich sind das aber einfach die Abweichungen von den beiden Population-Level Effects. sigma ist die Standardabweichung der Residuen. loadhi und loadlo sind die Mittelwerte der beiden Bedingungen.

m2 %>% 
  mcmc_plot("b")

Falls Sie die Verteilung der Differenz wollen, können Sie entweder das Modell so parametrisieren: ~ 1 + load + (1 | id), oder die Differenz nachträglich für jede Iteration berechnen. Dies können Sie so machen.

samples_m2 <- posterior_samples(m2) %>% 
    transmute(hi = b_loadhi,
              lo = b_loadlo, 
              Differenz = hi - lo)

Diese Differenz können Sie jetzt auch zusammenfassen

library(tidybayes)

samples_m2 %>% 
  select(Differenz) %>% 
  median_qi()

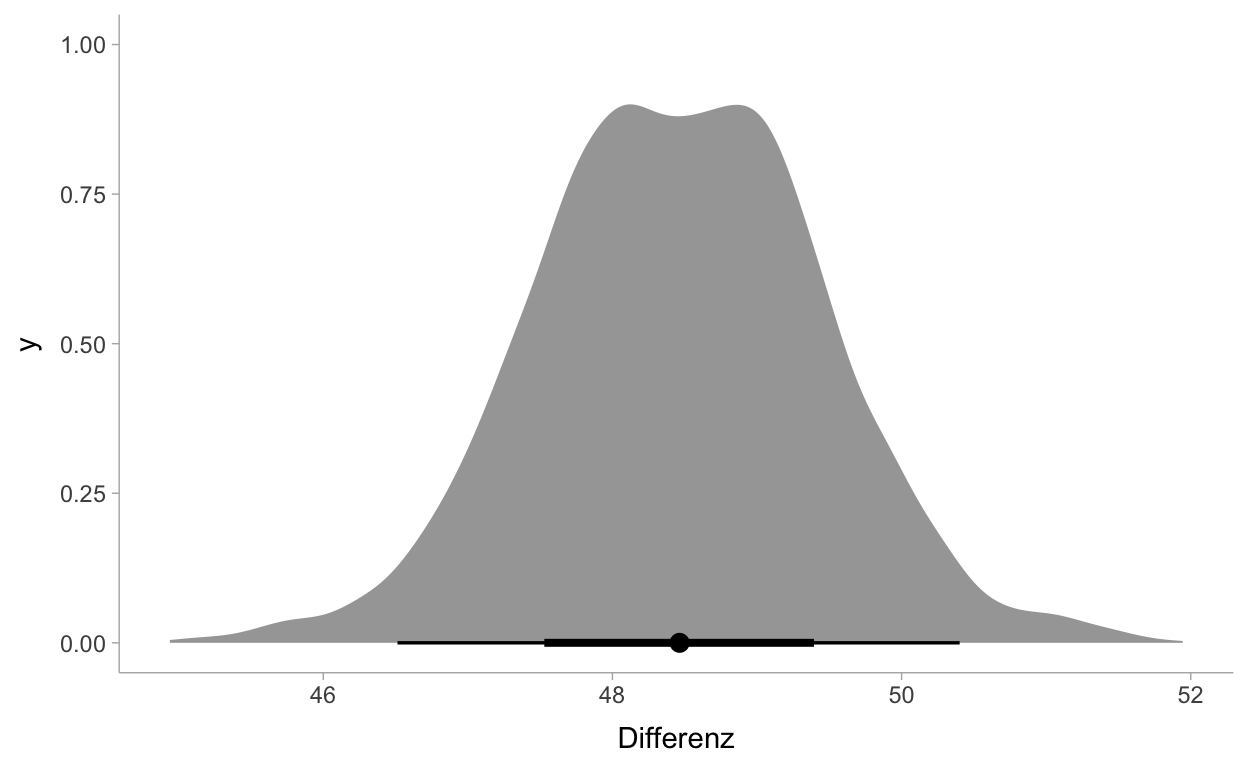
  Differenz   .lower  .upper .width .point .interval
1  48.46462 46.51335 50.4016   0.95 median        qi

und grafisch darstellen.

samples_m2 %>% 
  select(Differenz) %>% 
  ggplot(aes(x = Differenz)) +
  stat_halfeye(point_interval = median_qi) +
  theme_tidybayes()

Diskussion

Aufgabe 2.6

Auch hier dient dieser behaviorale Task dazu, die fMRI Analyse zu unterstützen. Wenn wir Unterschiedliche Aktivierung im präfrontalen Cortex in abhängigkeit des congitve load demonstrieren wollen, dann ist es vorteilhaft, auch behavioral einen Effekt zu zeigen.

Wir können wieder Angaben zur Posterior Verteilung der Parameter machen. Wir sind uns 95% sicher, dass die Differenz zwischen 46.54 und 50.39 liegt (das sind diejenigen Werte, welche am ehesten einen solchen Datensatz generienen). Weiter können wir sagen, welcher Anteil der Verteilung der Differenz positiv ist:

samples_m2 %>% 
  count(Differenz > 0) %>% 
  mutate(probability = n / sum(n))

  Differenz > 0    n probability
1          TRUE 4000           1

Oder wieder mit der hypothesis() Funktion:

m2 %>% 
  hypothesis("loadhi > loadlo")

Hypothesis Tests for class b:
             Hypothesis Estimate Est.Error CI.Lower CI.Upper
1 (loadhi)-(loadlo) > 0    48.46         1    46.86    50.06
  Evid.Ratio Post.Prob Star
1        Inf         1    *
---
'CI': 90%-CI for one-sided and 95%-CI for two-sided hypotheses.
'*': For one-sided hypotheses, the posterior probability exceeds 95%;
for two-sided hypotheses, the value tested against lies outside the 95%-CI.
Posterior probabilities of point hypotheses assume equal prior probabilities.

Die Wahrscheinlichkeit, dass in der high Bedingung die RTs grösser sind, ist also 1.

Auch hier müssen wir aber festhalten, dass wir noch keine Hypothese getestet haben. Dafür brauchen wir ein Nullmodell, in welchem wir die Load Bedingung weglassen (aud 0 fixieren).

Der grosse Unterschied zwischen Bayesianischer und frequentistischer Statistik ist (etwas vereinfacht) ausgedrückt:

Bei der frequentistischen Statistik erhalten wir nur eine Punktschätzung der Parameter, ohne etwas über deren Vereilung aussagen zu können (sie haben gar keine Verteilung). Wir würde evtl. gerne etwas darüber aussagen, aber wir dürfen nicht.

Bei der Bayesianischen Statistik erhalten wir eine Verteilung über alle möglichen Werte. Dies alleine erlaubt es uns schon, sehr informative Aussagen zu machen, bevor wir überhaupt daran denken, eine Hypothese mittels Modellvergleich zu testen.

Meule, Adrian. 2017. “Reporting and Interpreting Working Memory Performance in n-Back Tasks.” Frontiers in Psychology 8. https://doi.org/10.3389/fpsyg.2017.00352.

References

Corrections

If you see mistakes or want to suggest changes, please create an issue on the source repository.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY 4.0. Source code is available at https://github.com/kogpsy/neuroscicomplab, unless otherwise noted. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".

Citation

For attribution, please cite this work as

Ellis (2021, June 22). neuroscicomplab: Übung 2: Lösung. Retrieved from https://kogpsy.github.io/neuroscicomplab/solution-2.html

BibTeX citation

@misc{ellis2021übung,
  author = {Ellis, Andrew},
  title = {neuroscicomplab: Übung 2: Lösung},
  url = {https://kogpsy.github.io/neuroscicomplab/solution-2.html},
  year = {2021}
}

© Copyright 2021 Andrew Ellis

Software licensed under the Creative Commons Zero v4.0 Universal.