Übung 4: Lösung

Hypothesentest/Modelvergleich mit Bayes Factors.

Aufgabenstellung

Wir haben in Übung 2, Aufgabe 1 einen Datensatz untersucht, bei der Kinder mit einer ADHS Diagnose untersucht wurden. Das Ziel war es, die Arbeitsgedächtnisleistung dieser Kinder mit der Arbeitsgedächtnisleistung einer Kontrollgruppe zu vergleichen.

library(tidyverse)
nback1 <- read_csv("https://raw.githubusercontent.com/kogpsy/neuroscicomplab/main/data/adhd-nback.csv")

Die Gruppierungsvariable group zu einem Faktor konvertieren.

nback1 <- nback1 %>% 
  mutate(group = as_factor(group),
         group = fct_relevel(group, "control"))

Ein gerichteter Welch Test ergibt einen p-Wert von ca. 0.07. Dies bedeutet, dass wir unter Verwendung von \(\alpha = 0.05\) die Nullhypothese nicht ablehnen dürfen.

t.test(rt ~ group,
       data = nback1,
       alternative = "less")

    Welch Two Sample t-test

data:  rt by group
t = -1.5282, df = 28.57, p-value = 0.06873
alternative hypothesis: true difference in means between group control and group adhd is less than 0
95 percent confidence interval:
       -Inf 0.01757687
sample estimates:
mean in group control    mean in group adhd 
             1.153130              1.309528 

Wir wollen nun in dieser Übung die Parameter Bayesianisch schätzen, wie in Übung 2, aber diesmal mit dem Ziel, einen Hypothesentest durchzuführen.

Aufgabe 1

Schätzen Sie einen Achsenabschnitt und einen Unterschied zur Referenzkategorie. Wählen Sie einen normal(0, 1) Prior für den Unterschied zwischen den Gruppen.

summary(m1)

 Family: gaussian 
  Links: mu = identity; sigma = identity 
Formula: rt ~ group 
   Data: nback1 (Number of observations: 51) 
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup samples = 4000

Population-Level Effects: 
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept     1.15      0.06     1.03     1.28 1.00     3543     2601
groupadhd     0.16      0.10    -0.04     0.35 1.00     3581     2679

Family Specific Parameters: 
      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma     0.34      0.04     0.27     0.41 1.00     3673     2572

Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

Die beiden Population-Level Effects Intercept und groudadhd entsprechen dem erwarteten Wert der Kontrollgruppe, und dem erwartetent zwischen den Gruppen. Dieser hat einen Mittelwert von \(0.16\) mit einem \(95%\) Credible Interval von \([-0.04, 0.35]\).

In der Lösung von Übung 2 habe ich gezeigt, wie Sie mit der hypothesis() Funktion die Wahrscheinlichkeit erhalten, dass der Unterschied zwischen den Gruppen positiv ist.

Aufgabe 2

1. Wiederholen Sie dies hier, und beschreiben Sie bitte kurz das Resultat.

2. Speichern Sie den Output der hypothesis() Funktion und stellen Sie ihn mit plot() grafisch dar.

h1 <- m1 %>% 
  hypothesis("groupadhd > 0")

h1

Hypothesis Tests for class b:
       Hypothesis Estimate Est.Error CI.Lower CI.Upper Evid.Ratio
1 (groupadhd) > 0     0.16       0.1        0     0.31      17.18
  Post.Prob Star
1      0.94     
---
'CI': 90%-CI for one-sided and 95%-CI for two-sided hypotheses.
'*': For one-sided hypotheses, the posterior probability exceeds 95%;
for two-sided hypotheses, the value tested against lies outside the 95%-CI.
Posterior probabilities of point hypotheses assume equal prior probabilities.

Wir untersuchen hier, welcher Anteil der Posterior Verteilung des Gruppenunterschieds groupadhd positiv ist. Das Evidence Ratio Evid.Ratio gibt den Anteil der Fläche unter der Kurve, welcher positiv ist, geteilt durch den negativen Anteil. Wir erhalten ein Evidence Ratio von \(17.18\), was bedeutet, dass der positive Anteil der Fläche \(17.18\) mal grösser ist als der negative Anteil.

Folglich ist es \(17.18\) mal wahrscheinlicher, dass der Parameter positiv ist, als dass er negativ ist. Mit dieser Information können wir die Wahrscheinlichkeit, dass der Parameter positiv ist, berechnen. Wir müssen lediglich die Wahrscheinlichkeit \(p_+\) finden, für die gilt: \(\frac{p_+}{1-p_+} = 17.18\). Nach Umformen erhalten wir \(p_+ = 17.18/(1 + 17.18) = 0.945\). DIes ist genau die Wahrscheinlichkeit, welhe wir unter Post.Prob erhalten.

p_pos <- 17.18 / (1 + 17.18)
p_pos

[1] 0.9449945

plot(h1)

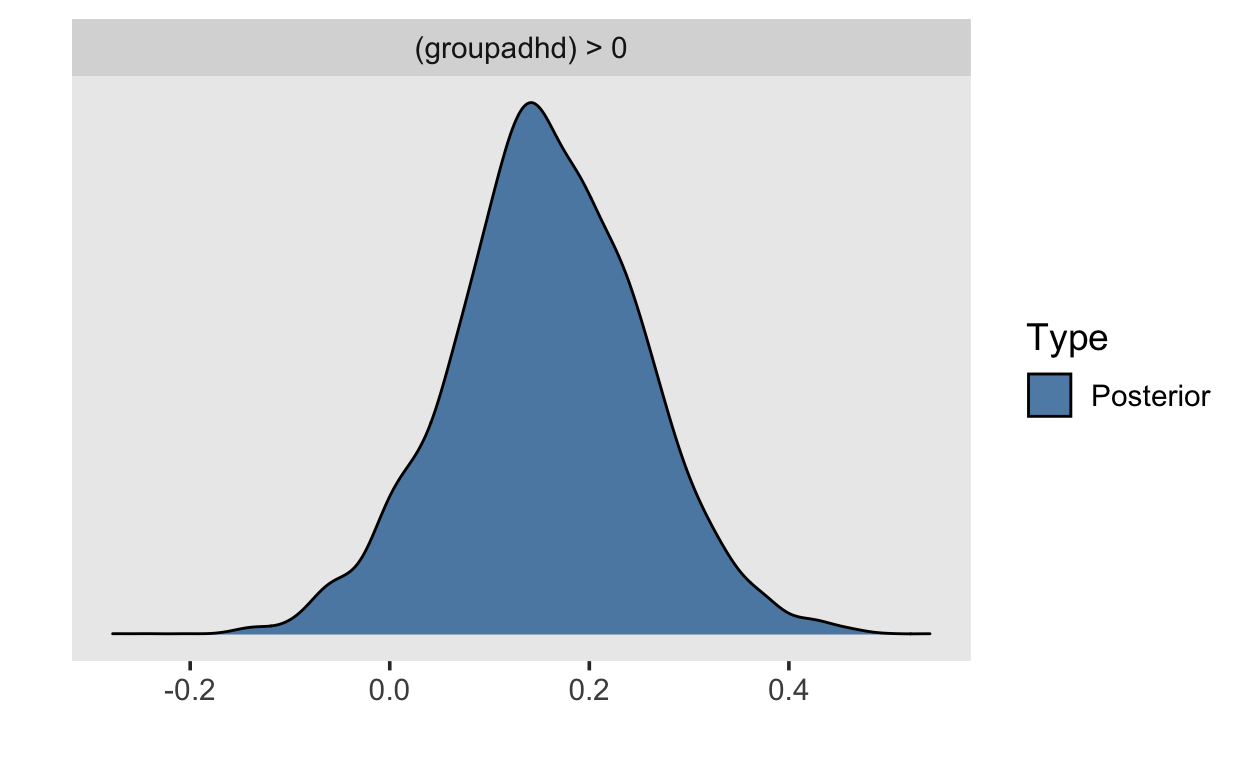
Aufgabe 3

Schätzen Sie das Modell von Aufgabe 1 nochmals, aber diesmal mit dem zusätzlichen Argument sample_prior = TRUE. Speichern Sie dies als m2.

m2 <- brm(rt ~ group,
          prior = priors,
          sample_prior = TRUE,
          data = nback1,
          file = "models/exc4-m2")

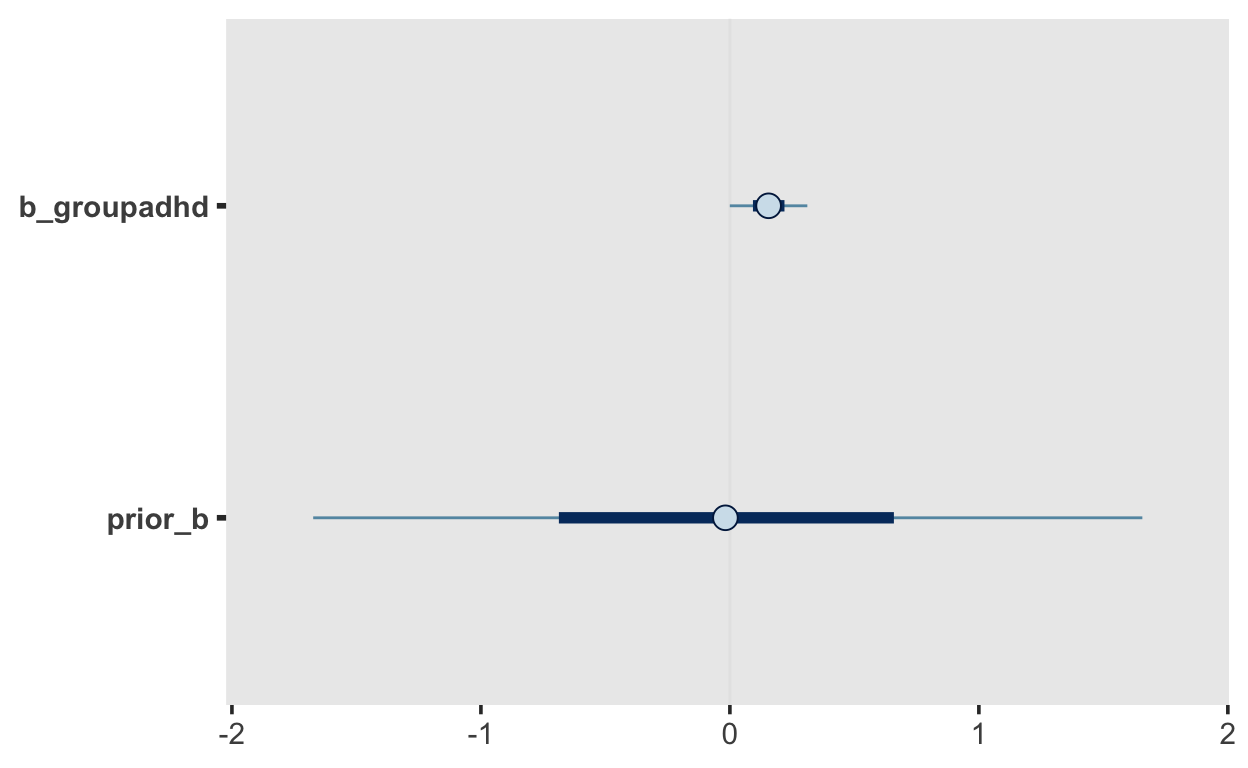
Dies führt dazu, dass Sie neben den Samples aus den Posterior Verteilung auch Samples aus den Prior Verteilungen erhalten. Diese können Sie für den Unterschied zwischen den Gruppen so grafisch darstellen.

m2 %>% 
  mcmc_plot(c("b_groupadhd", "prior_b"))

Wir sehen in dieser Grafik die Prior und die Posterior Verteilungen von b_groupadhd, also das, was wir anfangs geglaubt haben, und das, was wir glauben, nachdem wir die Daten berücksichtigt haben.

Aufgabe 4

Testen Sie nun die Nullhypothese, dass der Gruppenunterschied Null sein sollte, mit der hypothesis() Funktion (Savage-Dickey Density Ratio).

• Speichern Sie den Ouput als h2.
• Schauen Sie sich den Output an (mit print(h2) oder einfach h2.)
• Evidence Ratio Evid.Ratio ist der Bayes Factor \(BF_{01}\). Der Output der hypothesis() Funktion ist übrigens eine Liste; das Evid.Ratio kann mit h2$hypothesis$Evid.Ratio extrahiert werden. Speichern Sie es als BF01.
• Erklären Sie in Worten, was der \(BF_{01}\) bedeutet. Wofür haben Sie Evidenz gefunden?
• Zeigen Sie auch den Bayes Factor \(BF_{10}\) (Tipp: dies ist ganz einfach, wenn Sie \(BF_{01}\) haben). Was sagt uns \(BF_{10}\)?

h2 <- m2 %>% 
  hypothesis("groupadhd = 0")
h2

Hypothesis Tests for class b:
       Hypothesis Estimate Est.Error CI.Lower CI.Upper Evid.Ratio
1 (groupadhd) = 0     0.16       0.1    -0.03     0.34       2.63
  Post.Prob Star
1      0.72     
---
'CI': 90%-CI for one-sided and 95%-CI for two-sided hypotheses.
'*': For one-sided hypotheses, the posterior probability exceeds 95%;
for two-sided hypotheses, the value tested against lies outside the 95%-CI.
Posterior probabilities of point hypotheses assume equal prior probabilities.

BF01 <- h2$hypothesis$Evid.Ratio
BF01

[1] 2.62944

Der Bayes Factor \(BF_{01}\) gibt an, um wieviel wahrscheinlicher die Daten unter der Nullhypothese als unter der Alternativhypothese sind. Die Alternativhypothese entspricht unserem Prior, der besagt, dass der Unterschied zwischen den Gruppen mit 95% Sicherheit zwischen -2 und 2 liegt. Dieser Prior ist scheinbar nicht besonder gut, denn unter der Nullhypothese, welche behauptet, dass der Parameter genau 0 ist, sind die Daten ca. 2.6 mal wahrscheinlicher als unter der Alternativhypothese. Wir erhalten also hier Evidenz für die Nullhypothese, obwohl wir uns fas 95% sicher, dass der Parameter, wenn er geschätzt wird, positiv ist.

Der Bayes Factor für die Alternativhypothse beträgt \(0.38\).

BF10 <- 1/BF01
BF10

[1] 0.3803091

Aufgabe 5

Stellen Sie den Ouput von hypothesis() mit plot() grafisch dar.

Wir sehen, dass der WErt 0 unter dem Posterior eine höhere Wahrscheinlichkeit als unter dem Prior hat.

Optionale Aufgabe: Wie erhalten Sie einen grösseren Bayes Factor für die Alternativhypothese \(BF_{10}\)?

Wir können versuchen, einen sinnvolleren Prior für unsere Alternativhypothese zu defnieren. Als erstes könnten wir, wenn Informationen aus vorherigen Studien haben, erwarten dass der Effekt klein sein. Dies berücksichtigen wir mit einer kleineren Standardabweichung von \(0.1\). Ausserdem erwarten wir, dass der Effekt positiv wird. Dies können wir ausdrücken, in dem wir eine Untergrenze von 0 für die Prior Verteilung setzen (lower bound). Wenn wir beides komnbinieren, erhalten wir folgenden Prior: prior(normal(0, 0.1), lb = 0). Dies enstpricht einer halben Normalverteilung, mit einer Standardabweichung von \(0.1\).

m3 <- brm(rt ~ group,
          prior = prior(normal(0, 0.1), lb = 0),
          sample_prior = TRUE,
          data = nback1,
          file = "models/exc4-m3")

Wir können wieder Prior und Posterior grafisch darstellen. Der Prior erlaubt jetzt nur noch positive Werte.

m3 %>% 
  mcmc_plot(c("b_groupadhd", "prior_b"))

h3 <- m3 %>% 
  hypothesis("groupadhd = 0")
h3

Hypothesis Tests for class b:
       Hypothesis Estimate Est.Error CI.Lower CI.Upper Evid.Ratio
1 (groupadhd) = 0      0.1      0.06     0.01     0.22       0.42
  Post.Prob Star
1       0.3    *
---
'CI': 90%-CI for one-sided and 95%-CI for two-sided hypotheses.
'*': For one-sided hypotheses, the posterior probability exceeds 95%;
for two-sided hypotheses, the value tested against lies outside the 95%-CI.
Posterior probabilities of point hypotheses assume equal prior probabilities.

Wir erhalten nun einen Bayes Factor von $0.42 für die Nullhypothese. Dies bedeutet, dass nun die Daten unter der Alternativhypothese wahrscheinlicher sind.

BF01alt <- h3$hypothesis$Evid.Ratio
BF01alt

[1] 0.423604

Dies ist einfacher als \(BF_{10}\) auszudrücken:

BF10alt <- 1/BF01alt
BF10alt

[1] 2.360695

Wir erhalten nun also einen Bayes Factor von \(2.36\) für die Alternativhypothese.

Dies illustriert, dass ein Bayes Factor ausdrückt, wie gut ein e Prior Verteilung die Daten vorhersagen kann. Hypothesen entpsrechen im Bayesianischen Kontext Prior Verteilungen, und folglich müssen wir mit unseren Priors genau unsere Hypothesen ausdrücken können. Der zweite Bayes Factor \(BF_{10} = 2.36\) entspricht also unserer Erwartung, dass der Gruppenunterschied klein aber positiv ist.