Übung 1: Lösung

Schätzen des Parameters \(\theta\) einer Binomialverteilung.

Aufgabenstellung

Sie verabreichen einen Test, der aus 10 Fragen besteht. Die Fragen sind etwa gleich schwierig, und Sie sind sich sicher, dass die Fragen weder zu leicht noch zu schwierig für Ihre Schüler sind. Beim Betrachten der Resultate fällt Ihnen das Ergebnis eines Schülers besonders auf.

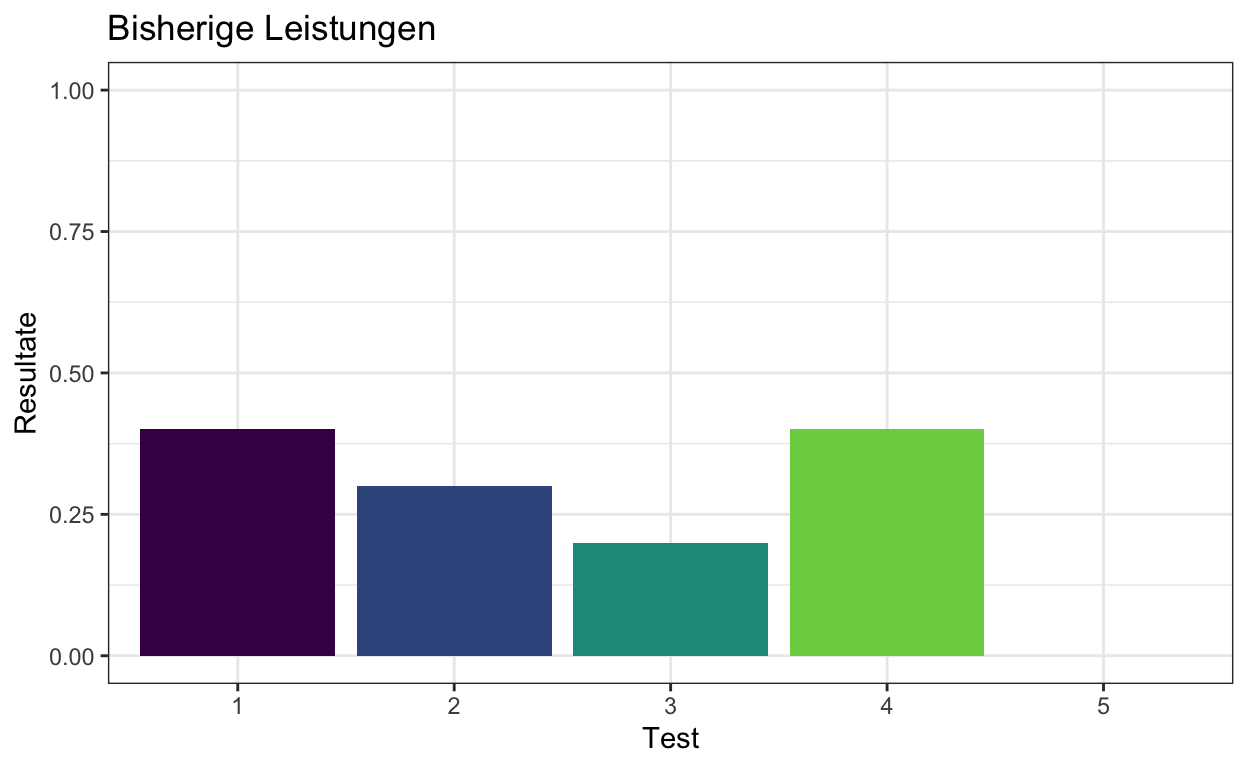
Bisher hatten Sie 4 solcher Tests verabreicht. Dieser Schüler schneidet normalerweise unterdurchschnittlich ab, mit Ergebnissen von \(4/10\), \(3/10\), \(2/10\) und \(4/10\) richtigen Antworten. Sie haben sich schon vorgenommen, die Elter des Schülers zu kontaktieren, da Sie sich Sorgen machen.

library(tidyverse)

Im folgenden werden die vorherigen 4 Testresultate als Balkendiagramm dargestellt. Die Leistungen des Schülers sehen nicht besonders befriedigend aus.

tibble(Test = as_factor(1:5), Resultate = c(4/10, 3/10, 2/10, 4/10, NA)) %>% 
  ggplot(aes(Test, Resultate, fill = Test)) +
  geom_bar(stat = 'identity') +
  scale_fill_viridis_d(end = 0.8) +
  scale_y_continuous(limits = c(0, 1)) +
  theme_bw() +
  theme(legend.position = "none") +
  ggtitle("Bisherige Leistungen")

Beim aktuellen Test sehen die Antworten aber so aus:

answers <- c(1, 1, 1, 1, 0, 1, 1, 1, 1, 1)

1 bedeutet, die Frage wurde richtig beantwortet, 0 steht für eine inkorrekte Antwort.

Berechnen Sie die Anzahl korrekter Antworten, sowie die Anzahl korrekter Antworten in den bisherigen Tests.

ncorrect <- sum(answers)
nquestions <- length(answers)
prior_ncorrect <- 4 + 3 + 2 + 4
prior_nquestions <- 4 * 10
prior_nwrong <- prior_nquestions - prior_ncorrect

Sie freuen sich—vielleicht hat sich der Schüler bei diesem Test besonders Mühe gegeben. Sie überlegen sich, ob Sie nun warten sollen, oder doch mit den Eltern einen Termin für ein Gespräch abmachen sollen.

Vielleicht kann Ihnen Bayesianische Inferenz helfen?

Aufgaben

Versuchen Sie, mit Hilfe Ihres Vorwissens über die Leistungen des Schülers seine Fähigkeit (ability), Fragen richtig zu beantworten, zu schätzen. Da Sie wissen, dass Sie die Fähigkeit nur ungenau schätzen können, wollen Sie Ihre Unsicherheit mit einer Posterior Distribution quantifizieren.

Wir definieren zuerst einen Vektor, der alle möglichen Werte des Parameters \(\theta\) enthält, d.h. alle Werte zwischen 0 und 1. Da wir hier genau sein wollen, nehmen wir 100 Zahlen zwischen 0 und 1—an diesen Stellen wollen wir die Prior- und Posterior Wahrscheinlichkeiten untersuchen.

n_points <- 100
theta_grid <- seq(from = 0 , to = 1 , length.out = n_points)
theta_grid

  [1] 0.00000000 0.01010101 0.02020202 0.03030303 0.04040404
  [6] 0.05050505 0.06060606 0.07070707 0.08080808 0.09090909
 [11] 0.10101010 0.11111111 0.12121212 0.13131313 0.14141414
 [16] 0.15151515 0.16161616 0.17171717 0.18181818 0.19191919
 [21] 0.20202020 0.21212121 0.22222222 0.23232323 0.24242424
 [26] 0.25252525 0.26262626 0.27272727 0.28282828 0.29292929
 [31] 0.30303030 0.31313131 0.32323232 0.33333333 0.34343434
 [36] 0.35353535 0.36363636 0.37373737 0.38383838 0.39393939
 [41] 0.40404040 0.41414141 0.42424242 0.43434343 0.44444444
 [46] 0.45454545 0.46464646 0.47474747 0.48484848 0.49494949
 [51] 0.50505051 0.51515152 0.52525253 0.53535354 0.54545455
 [56] 0.55555556 0.56565657 0.57575758 0.58585859 0.59595960
 [61] 0.60606061 0.61616162 0.62626263 0.63636364 0.64646465
 [66] 0.65656566 0.66666667 0.67676768 0.68686869 0.69696970
 [71] 0.70707071 0.71717172 0.72727273 0.73737374 0.74747475
 [76] 0.75757576 0.76767677 0.77777778 0.78787879 0.79797980
 [81] 0.80808081 0.81818182 0.82828283 0.83838384 0.84848485
 [86] 0.85858586 0.86868687 0.87878788 0.88888889 0.89898990
 [91] 0.90909091 0.91919192 0.92929293 0.93939394 0.94949495
 [96] 0.95959596 0.96969697 0.97979798 0.98989899 1.00000000

Aufgabe 1

Berechnen Sie nun die Wahrscheinlichkeit, das Testergebnis des Schülers zu erreichen, d.h. die Wahrscheinlichkeit der Daten für jeden möglichen Parameterwert.

Wir wollen hier für jeden möglichen \(\theta\)-Wert wissen, was die Wahrscheinlichkeit wäre, gegeben diesen Wert, 9 von 10 Fragen richtig zu beantworten.

likelihood <- dbinom(x = ncorrect , size = nquestions , prob = theta_grid)

Der \(\theta\)-Wert, für den diese Wahrscheinlichkeit am grössten ist, ist die Maximum-Likelihood Schätzung für die Wahrscheinlichkeit des Schülers, eine Frage richtig zu beantworten (Diese Wahrscheinlichkeit verstehen wir als Fähigkeit des Schülers).

Sie können diese Wahrscheinlichkeit so graphisch darstellen.

tibble(theta_grid, likelihood) %>% 
  ggplot(aes(x = theta_grid, y = likelihood)) +
  geom_line()

Aufgabe 2

Wenn Sie kein Vorwissen über die bisherigen Testresultate des Schülers hätten: Was würden Sie als Schätzung der Fähigkeit des Schülers benutzen?

Sie haben nur das aktuelle Resultat zur Verfügung (9 richtige Antowrten in 10 Fragen).

Wenn wir nur den aktuellen Test haben, können wir entweder diese Maximum-Likelihood Schätzung nehmen, oder unser fehlendes Vorwissen als uniformen Prior über \(\theta\) ausdrücken.

Maximum-Likelihood Schätzung

Wir suchen zuerst die grösste Wahrscheinlichkeit:

maxlik <- max(likelihood)

Und suchen dann den Wert im theta_grid, für welchen die Wahrscheinlichkeit der grössten Wahrscheinlichkeit entspricht.

theta_maxlik <- theta_grid[likelihood == maxlik]
theta_maxlik

[1] 0.8989899

Dieser Wert beträgt hier 0.8989899. Natürlich wissen wir, dass dieser Wert \(9/10\) beträgt—diese Ungenauigkeit ist eine Folge der Grid Approximation.

Aufgabe 3

Versuchen Sie nun, Ihr Vorwissen über die Leistungen des Schülers in Form einer Prior-Verteilung auszudrücken.

Hier benutzen wir unsere bisherigen Testergebnisse. Die Parameter der Beta Verteilung können so verstanden werden. \(\alpha\) entspricht den bisherigen Erfolgen, und \(\beta\) den bisherigen Misserfolgen. Die Erfolgen waren \(4 + 3 + 2 + 4\), oder prior_ncorrect, die Misserfolge prior_ncorrect ergeben sich aus der Anzahle Fragen minus der Anzahl Erfolge.

prior <- dbeta(x = theta_grid, shape1 = prior_ncorrect,  shape2 = prior_nquestions)

Was wir hier sehen, ist dass Bayes Theorem sequentiell anwendbar ist: wir könnten die Anzahl richtiger und falscher Antworten aus dem ersten Test als Prior für den zweiten Test verwenden, oder die ersten beiden Tests als Prior für den dritten. Solange wir dieselbe Information benutzen, und dieselben Daten, erhalten wir immer dasselbe Ergebnis.

Aufgabe 4

Berechnen Sie die Posterior-Verteilung als Produkt von Likelihood und Ihrem Prior.

Die nicht normalisierte Posterior Verteilung erhalten wir einfach durch Multiplikation von Prior und Likelihood.

\[ P(\theta|Data) \propto P(Data|\theta) * P(\theta) \]

oder

\[ \text{posterior} \propto \text{likelihood} * \text{prior} \]

Einfach ausgedrückt: Der Posterior Belief für jeden Wert von theta_grid ist das Produkt dessen A-Priori Wahrscheinlichkeit und der Wahrscheinlichkeit, gegeben diesen Wert, ein Ergebnis von \(9/10\) zu erhalten.

unstandardized_posterior <- likelihood * prior

posterior <- unstandardized_posterior / sum(unstandardized_posterior)

posterior

  [1] 0.000000e+00 6.274344e-27 8.730208e-21 2.876875e-17 7.956634e-15
  [6] 5.649494e-13 1.694414e-11 2.799608e-10 2.985869e-09 2.276766e-08
 [11] 1.330839e-07 6.267273e-07 2.466616e-06 8.342069e-06 2.477257e-05
 [16] 6.570724e-05 1.578224e-04 3.471417e-04 7.057464e-04 1.336443e-03
 [21] 2.372678e-03 3.971135e-03 6.295506e-03 9.491909e-03 1.365878e-02
 [26] 1.881630e-02 2.488170e-02 3.165660e-02 3.883094e-02 4.600498e-02
 [31] 5.272727e-02 5.854333e-02 6.304737e-02 6.592885e-02 6.700649e-02
 [36] 6.624502e-02 6.375288e-02 5.976255e-02 5.459769e-02 4.863312e-02
 [41] 4.225378e-02 3.581839e-02 2.963157e-02 2.392676e-02 1.885989e-02
 [46] 1.451238e-02 1.090121e-02 7.993079e-03 5.720031e-03 3.994323e-03
 [51] 2.721063e-03 1.807792e-03 1.170873e-03 7.389786e-04 4.542499e-04
 [56] 2.717996e-04 1.582021e-04 8.950946e-05 4.918894e-05 2.623114e-05
 [61] 1.356082e-05 6.788842e-06 3.287152e-06 1.537365e-06 6.934682e-07
 [66] 3.012052e-07 1.257493e-07 5.036111e-08 1.930546e-08 7.066534e-09
 [71] 2.463225e-09 8.152145e-10 2.553044e-10 7.537708e-11 2.089257e-11
 [76] 5.410801e-12 1.302339e-12 2.895595e-13 5.905869e-14 1.096211e-14
 [81] 1.834675e-15 2.739119e-16 3.602244e-17 4.111162e-18 3.999822e-19
 [86] 3.246715e-20 2.141543e-21 1.110912e-22 4.348794e-24 1.218191e-25
 [91] 2.276766e-27 2.582225e-29 1.555934e-31 4.099371e-34 3.491487e-37
 [96] 5.795897e-41 7.262254e-46 8.164537e-53 9.210282e-65 0.000000e+00

Aufgabe 5

Stellen Sie Prior, Likelihood und Posterior grafisch dar

df <- tibble(theta_grid, prior, likelihood, posterior)

df %>%
  pivot_longer(-theta_grid, names_to = "distribution", values_to = "density") %>% 
  mutate(distribution = as_factor(distribution)) %>% 
  ggplot(aes(theta_grid, density, color = distribution)) +
  geom_line(size = 1.5) +
  geom_vline(xintercept = 9/10, linetype = "dashed") +
  scale_color_viridis_d(end = 0.8) +
  xlab("Theta Werte") +
  ylab("") +
  facet_wrap(~distribution, scales = "free_y") +
  theme_bw()

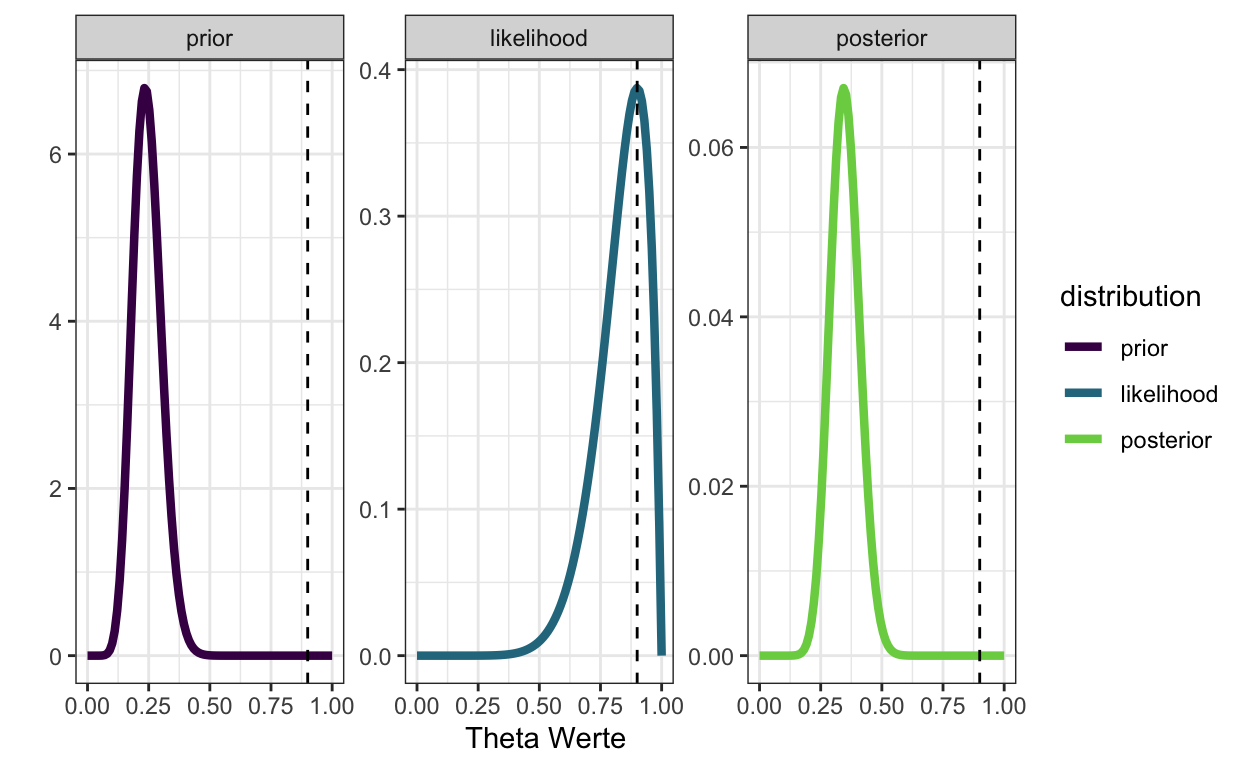
Wenn wir unseren Prior Belief durch eine Beta Verteilung mit den bisherigen Ergebnissen als Parameter \(\alpha\) und \(\beta\) ausdrücken, dann ist unsere Posterior Verteilung ziemlich weit weg von von der Maximum-Likelihood Schätzung (gestrichelte Linie)—unser Vorwissen wird hier stark gewichtet, so dass das aktuelle Testergebnis eine geringe Auswirkung auf den Posterior hat.

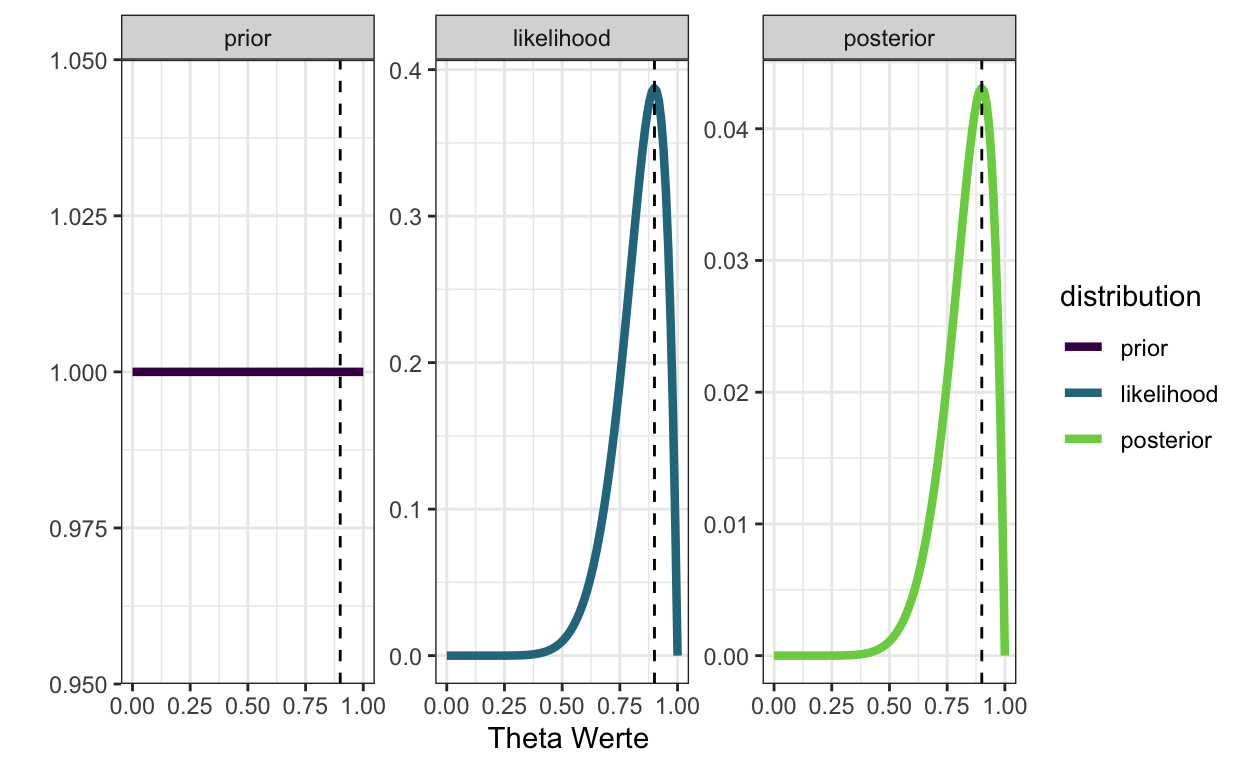
Wenn wir im Vergleich dazu einen uniformen Prior benutzen, liegt der höchste Wert des Posteriors auf der Maximum-Likelihood Linie. Der Posterior sieht genau gleich aus wie die Likelihood, weil die Likelihood die einzige Informationsquelle ist.

prior <- dbeta(x = theta_grid, shape1 = 1,  shape2 = 1)
unstandardized_posterior <- likelihood * prior
posterior <- unstandardized_posterior / sum(unstandardized_posterior)

tibble(theta_grid, prior, likelihood, posterior) %>%
  pivot_longer(-theta_grid, names_to = "distribution", values_to = "density") %>% 
  mutate(distribution = as_factor(distribution)) %>% 
  ggplot(aes(theta_grid, density, color = distribution)) +
  geom_line(size = 1.5) +
  geom_vline(xintercept = 9/10, linetype = "dashed") +
  scale_color_viridis_d(end = 0.8) +
  xlab("Theta Werte") +
  ylab("") +
  facet_wrap(~distribution, scales = "free_y") +
  theme_bw()

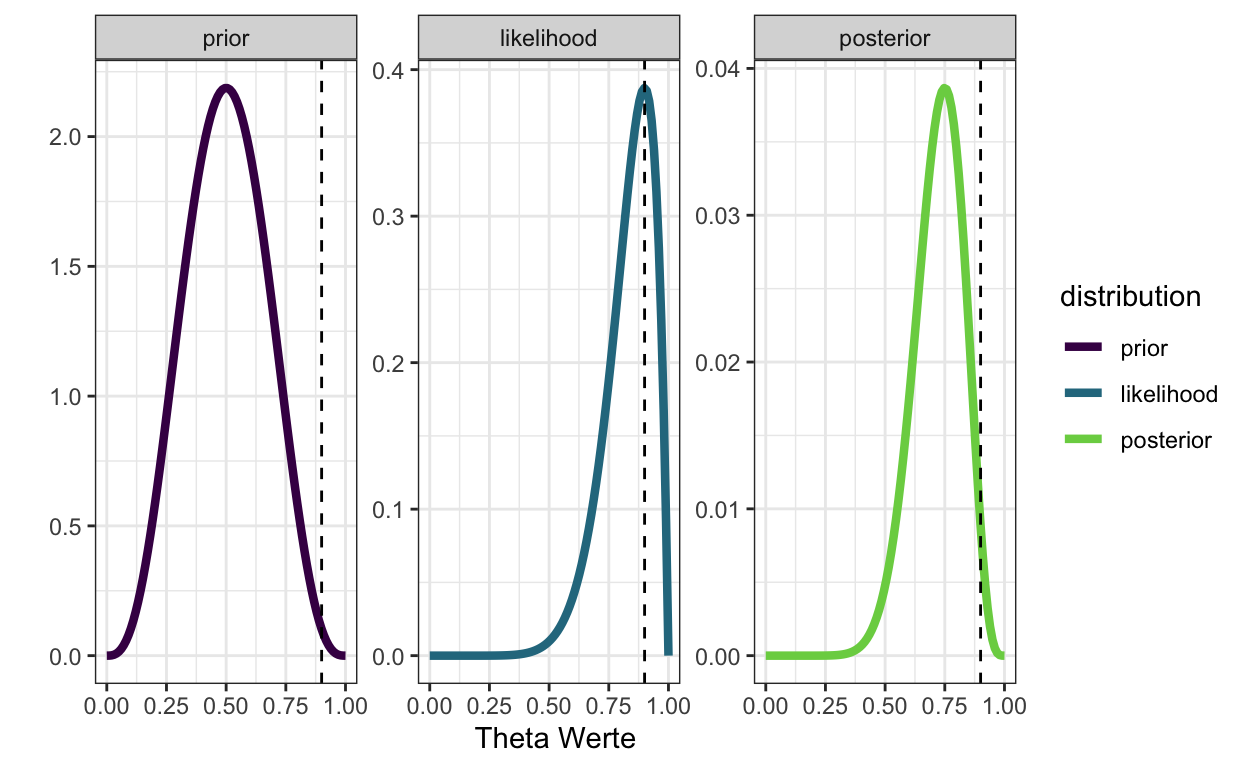
Wenn wir annehmen, der Schüler sei nicht ganz so schlecht, wie die bisherigen Testergebnisse vermuten lassen, können wir einen Beta(4, 4) Prior anehmen. Dieser drückt aus, dass wir erwarten, das der Schüler ungefähr die Hälfte der Fragen richtig beantworten kann. Dann liegt der Posterior links neben der Likelihood.

prior <- dbeta(x = theta_grid, shape1 = 4,  shape2 = 4)
unstandardized_posterior <- likelihood * prior
posterior <- unstandardized_posterior / sum(unstandardized_posterior)

tibble(theta_grid, prior, likelihood, posterior) %>%
  pivot_longer(-theta_grid, names_to = "distribution", values_to = "density") %>% 
  mutate(distribution = as_factor(distribution)) %>% 
  ggplot(aes(theta_grid, density, color = distribution)) +
  geom_line(size = 1.5) +
  geom_vline(xintercept = 9/10, linetype = "dashed") +
  scale_color_viridis_d(end = 0.8) +
  xlab("Theta Werte") +
  ylab("") +
  facet_wrap(~distribution, scales = "free_y") +
  theme_bw()

Aufgabe 6

Was ist die Warscheinlichkeit, dass jemand mit solchen Vorleistungen mindestens 9 Fragen von 10 beantwortet, falls die Vorleistungen tatsächlich die wahre Fähigkeiten der Schüler messen?

Hier ist die kumulative Wahrscheinlichkeit gefragt, 9 oder 10 Fragen richtig zu beantworten, und zwar bevor wir die neuen Daten des Schülers berücksichtigen.

Diese kumulative Wahrscheinlichkeit können wir mit der Funktion pbinom berechnen. Wir nehmen hier an, die Punktschätzung von 0.325 aus den bisherigen Tests genügt hier. Falls wir hier schon eine Posterior Verteilung aus den ersten 4 Tests hätten, könnten wir damit unsere Unsicherheit ausdrücken—diese Verteilung fehlt uns aber hier.

Wir berechen zuerst die kumulative Wahrscheinlichkeit 1, 2, 3, 4, 5, 6, 7 oder 8 Fragen richtig zu beantworten:

pbinom(q = ncorrect-1,
       size = nquestions, 
       prob = prior_ncorrect/prior_nquestions)

[1] 0.9997138

Diese Wahrscheinlichkeit ist 0.9997

Die Wahrscheinlichkeit, mehr als 8 Fragen richtig zu beantworten, ist

1 - pbinom(q = ncorrect-1, 
           size = nquestions, 
           prob = prior_ncorrect/prior_nquestions)

[1] 0.0002862047

oder

pbinom(q = ncorrect-1, 
       size = nquestions, 
       prob = prior_ncorrect/prior_nquestions,
       lower.tail = FALSE)

[1] 0.0002862047

und beträgt ungefähr 3^{-4}. Wir sind also sehr überrascht, wenn dieser Schüler plötzlich so viele Fragen richtig beantwortet. Vielleicht hatte der Schüler sich vorher keine Mühe gegeben, oder nicht gelernt—in diesem Fall wäre unsere Schätzung seiner Fähigkeit schlecht, und müsste revidiert werden. Eine andere Möglichkeit ist, dass der Schüler geschummelt hat—die Frage können wir hier aber nicht beantworten.

Eine andere Möglichkeit, die kumulative Wahrscheinlichkeit zu berechnen, ist einfach die Wahrscheinlichkeiten von 9 und von 10 Richtigen zu addieren.

dbinom(x = 9, 
       size = nquestions, 
       prob = prior_ncorrect/prior_nquestions) +
  dbinom(x = 10, 
       size = nquestions, 
       prob = prior_ncorrect/prior_nquestions) 

[1] 0.0002862047

oder

sum(dbinom(x = 9:10, 
       size = nquestions, 
       prob = prior_ncorrect/prior_nquestions))

[1] 0.0002862047

Bemerkung

Einige von Ihnen haben versucht, den Posterior zusammenzufassen, z.B. so:

sum(posterior[theta_grid > 0.9])

[1] 0.01870636

Dies ist natürlich möglich, beantwortet aber eine andere Frage, und zwar: Was ist die Posterior Wahrscheinlichkeit von \(\theta\), gegeben unsere Prior Beliefs und das Testresultat? Die Frage in Aufgabe 6 lautete aber: Was ist die Wahrscheinlichkeit, gegeben der Fähigkeit des Schülers, dass er 9 oder 10 Fragen richtig beantwortet? Das wäre die Frage, die wir uns stellen, wenn wir frequentistische Statistik machen—die Frage nach der Wahrscheinlichkeit der Parameter dürfen wir uns dann gar nicht stellen.