Übung 4: Lösung

Hypothesentest/Modelvergleich mit Bayes Factors.

Die Aufgaben, die Sie bearbeiten sollen, finden Sie in einem gelben Kasten. Optionale Aufgaben sind in orangen Kästen.

Sie haben für diese Übung 8 Tage Zeit. Laden Sie Ihre Lösung als Rmarkdown File bis Mittwoch, 28. April um 00:00 Uhr, in den Order für Übung 4 auf ILIAS. Falls Rmarkdown nicht funkionieren sollte, werden auch Lösungen in Form eines R Skriptes akzeptiert. Nennen Sie Ihr File Matrikelnummer_Nachname_uebung-4.Rmd oder Matrikelnummer_Nachname_uebung-4.R, z. B. 15-172-874_Nachname_uebung-4.Rmd.

Bevor Sie einreichen, vergewissern Sie sich bitte, dass Ihr Rmarkdown File geknittet werden kann, und dass der R Code ohne Fehler läuft.

Aufgabenstellung

Wir haben in Übung 2, Aufgabe 1 einen Datensatz untersucht, bei der Kinder mit einer ADHS Diagnose untersucht wurden. Das Ziel war es, die Arbeitsgedächtnisleistung dieser Kinder mit der Arbeitsgedächtnisleistung einer Kontrollgruppe zu vergleichen.

library(tidyverse)
nback1 <- read_csv("https://raw.githubusercontent.com/kogpsy/neuroscicomplab/main/data/adhd-nback.csv")

Die Gruppierungsvariable group sollte zu einem Faktor konvertiert werden.

nback1 <- nback1 %>% 
  mutate(group = as_factor(group),
         group = fct_relevel(group, "control"))

Ein gerichteter Welch Test ergibt einen p-Wert von ca. 0.07. Dies bedeutet, dass wir unter Verwendung von \(\alpha = 0.05\) die Nullhypothese nicht ablehnen dürfen.

t.test(rt ~ group,
       data = nback1,
       alternative = "less")

    Welch Two Sample t-test

data:  rt by group
t = -1.5282, df = 28.57, p-value = 0.06873
alternative hypothesis: true difference in means between group control and group adhd is less than 0
95 percent confidence interval:
       -Inf 0.01757687
sample estimates:
mean in group control    mean in group adhd 
             1.153130              1.309528 

Wir wollen nun in dieser Übung die Parameter Bayesianisch schätzen, wie in Übung 2, aber diesmal mit dem Ziel, einen Hypothesentest durchzuführen.

Aufgabe 1

Schätzen Sie einen Achsenabschnitt und einen Unterschied zur Referenzkategorie. Wählen Sie einen normal(0, 1) Prior für den Unterschied zwischen den Gruppen.

library(brms)

Wir unterscuhen zuerst mit der get_prior() Funktion, welche Priors für dieses Modell möglich sind und was brms als Default Prior definiert.

Da der Ouput sonst zu lang ist, nehme ich hier mit select() nur die ersten vier Spalten.

default_priors <- get_prior(rt ~ 1 + group,
          data = nback1)

default_priors %>% 
  as_tibble() %>% 
  select(1:4)

# A tibble: 4 x 4
  prior                    class     coef        group
  <chr>                    <chr>     <chr>       <chr>
1 ""                       b         ""          ""   
2 ""                       b         "groupadhd" ""   
3 "student_t(3, 1.2, 2.5)" Intercept ""          ""   
4 "student_t(3, 0, 2.5)"   sigma     ""          ""   

Wie erwartet ist der Default Prior für den Koeffizienten b_groupadhd flach (dies erkennt man daran, dass kein Prior definiert wird, so dass rstan dann einen flachen Prior benutzt). Wir defnieren nun eine Normalverteilung mit \(\mu = 0\) und \(\sigma = 1\) als Prior für den Unterschied zwischen den Gruppen.

priors <- prior(normal(0, 1), class = b)

In der Lösung von Übung 2 habe ich gezeigt, wie Sie mit der hypothesis() Funktion die Wahrscheinlichkeit erhalten, dass der Unterschied zwischen den Gruppen positiv ist.

Aufgabe 2

1. Wiederholen Sie dies hier, und beschreiben Sie bitte kurz das Resultat.

2. Speichern Sie den Output der hypothesis() Funktion und stellen Sie ihn mit plot() grafisch dar.

h1 <- m1 %>% 
  hypothesis(___)

Aufgabe 3

Schätzen Sie das Modell von Aufgabe 1 nochmals, aber diesmal mit dem zusätzlichen Argument sample_prior = TRUE. Speichern Sie dies als m2.

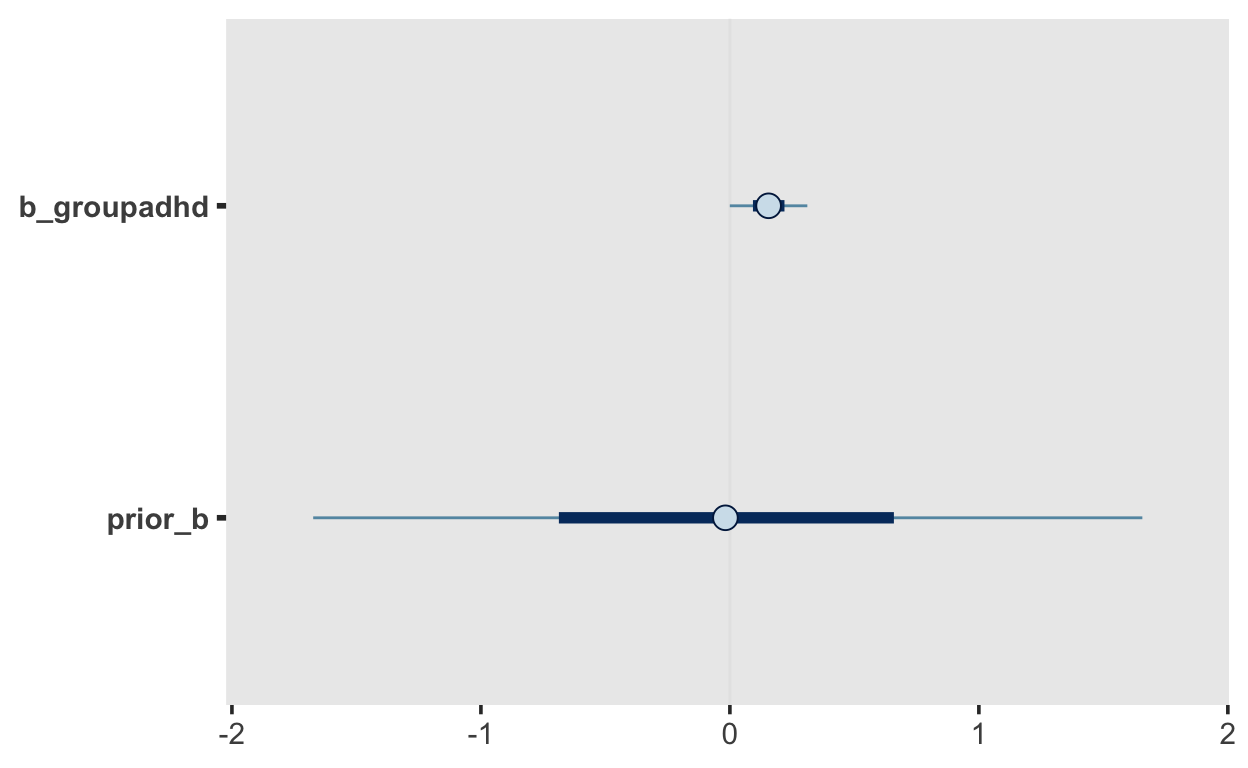
Dies führt dazu, dass Sie neben den Samples aus den Posterior Verteilung auch Samples aus den Prior Verteilungen erhalten. Diese können Sie für den Unterschied zwischen den Gruppen so grafisch darstellen.

m2 %>% 
  mcmc_plot(c("b_groupadhd", "prior_b"))

Aufgabe 4

Testen Sie nun die Nullhypothese, dass der Gruppenunterschied Null sein sollte, mit der hypothesis() Funktion (Savage-Dickey Density Ratio).

• Speichern Sie den Ouput als h2.
• Schauen Sie sich den Output an (mit print(h2) oder einfach h2.)
• Evidence Ratio Evid.Ratio ist der Bayes Factor \(BF_{01}\). Der Output der hypothesis() Funktion ist übrigens eine Liste; das Evid.Ratio kann mit h2$hypothesis$Evid.Ratio extrahiert werden. Speichern Sie es als BF01.
• Erklären Sie in Worten, was der \(BF_{01}\) bedeutet. Wofür haben Sie Evidenz gefunden?
• Zeigen Sie auch den Bayes Factor \(BF_{10}\) (Tipp: dies ist ganz einfach, wenn Sie \(BF_{01}\) haben). Was sagt uns \(BF_{10}\)?

h2 <- m2 %>% 
  hypothesis(___)

Aufgabe 5

Stellen Sie den Ouput von hypothesis() mit plot() grafisch dar.

Optionale Aufgabe: Wie erhalten Sie einen grösseren Bayes Factor für die Alternativhypothese \(BF_{10}\)?