neuroscicomplab: Einführung

Andrew Ellis

Klassische (frequentistische) Statistik

Im Verlauf Ihres bisherigen Studiums haben Sie verschiedene statistische Methode kennengelernt, die alle etwas mit Null Hypothesis Significance Testing (NHST) zu haben. Diese Verfahren haben gemeinsam, dass sie

Punktschätzungen von Parametern benutzen
mit diesen Punktschätzungen eine Teststatistik erstellen
die Wahrscheinlichkeit angeben, mit derer eine mindestens so extreme Ausprägung dieser Teststatistik erreicht wird, unter der Annahme, dass die Nullhypothese wahr ist. Diese Wahrscheinlichkeit nennt man einen p-Wert.

Diese Methoden stehen schon seit längerem in der Kritik:

Gigerenzer (2004);Gigerenzer (2018) behauptet unter anderem, dass die Verwendung von NHST Methoden oftmals einem statistischen Ritual gleichkommt.
Wasserstein and Lazar (2016) schreiben im Statement on Statistical Significance and P-Values der American Statistical Association:
- P-values can indicate how incompatible the data are with a specified statistical model.
- P-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone.
- Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold.

Es scheint also grosse Probleme mit dem Verständnis von Konzepten der klassischen Statistik zu geben. Zum Beispiel werden Grundlegende Konzepte wie p-Werte und Konfidenzintervalle oft falsch verstanden (Hoekstra et al. 2014).

Beispiel: t-Test

Schauen wir uns das Beispiel der letzten Sitzung nochmals an. Wir haben einen Datensatz generiert, um zwei geschätzte Mittelwerte zu vergleichen, mit dem Ziel herauszufinden, ob eine Gruppe einen grösseren Mittelwert als die andere hat.

library(tidyverse)
library(kableExtra)

set.seed(12)

# Number of people wearing fancy hats
N_fancyhats <- 50 

# Number of people not wearing fancy hats
N_nofancyhats <- 50

# Population mean of creativity for people wearing fancy hats
mu_fancyhats <- 103 

# Population mean of creativity for people wearing no fancy hats
mu_nofancyhats <- 98 

# Average population standard deviation of both groups
sigma <- 15 

# Generate data
fancyhats = tibble(Creativity = rnorm(N_fancyhats, mu_fancyhats, sigma),
               Group = "Fancy Hat")

nofancyhats = tibble(Creativity = rnorm(N_nofancyhats, mu_nofancyhats, sigma),
                 Group = "No Fancy Hat")


FancyHat <- bind_rows(fancyhats, nofancyhats)  %>%
    mutate(Group = fct_relevel(as.factor(Group), "No Fancy Hat"))

Die Daten sehen so aus:

kbl(FancyHat) %>%
  kable_paper() %>%
  scroll_box(width = "500px", height = "200px")

Creativity	Group
80.79149	Fancy Hat
126.65754	Fancy Hat
88.64883	Fancy Hat
89.19992	Fancy Hat
73.03537	Fancy Hat
98.91556	Fancy Hat
98.26977	Fancy Hat
93.57617	Fancy Hat
101.40304	Fancy Hat
109.42022	Fancy Hat
91.33421	Fancy Hat
83.59177	Fancy Hat
91.30650	Fancy Hat
103.17928	Fancy Hat
100.71376	Fancy Hat
92.44804	Fancy Hat
120.83319	Fancy Hat
108.10768	Fancy Hat
110.60452	Fancy Hat
98.60042	Fancy Hat
106.35462	Fancy Hat
133.10802	Fancy Hat
118.17969	Fancy Hat
98.46311	Fancy Hat
87.62133	Fancy Hat
98.98923	Fancy Hat
100.01342	Fancy Hat
104.96684	Fancy Hat
105.18700	Fancy Hat
108.43097	Fancy Hat
113.10972	Fancy Hat
134.08054	Fancy Hat
94.88457	Fancy Hat
86.94262	Fancy Hat
97.41315	Fancy Hat
95.72288	Fancy Hat
107.12176	Fancy Hat
95.80731	Fancy Hat
114.97158	Fancy Hat
87.93323	Fancy Hat
104.57476	Fancy Hat
85.66011	Fancy Hat
111.67202	Fancy Hat
79.06562	Fancy Hat
98.37245	Fancy Hat
109.74199	Fancy Hat
88.34420	Fancy Hat
105.84997	Fancy Hat
113.97180	Fancy Hat
95.61101	Fancy Hat
97.35973	No Fancy Hat
96.30994	No Fancy Hat
104.85241	No Fancy Hat
128.30502	No Fancy Hat
82.23665	No Fancy Hat
109.01978	No Fancy Hat
106.08875	No Fancy Hat
78.28591	No Fancy Hat
94.24942	No Fancy Hat
102.71307	No Fancy Hat
104.09820	No Fancy Hat
112.91631	No Fancy Hat
110.83653	No Fancy Hat
100.95693	No Fancy Hat
110.51488	No Fancy Hat
110.70185	No Fancy Hat
127.31158	No Fancy Hat
65.76110	No Fancy Hat
112.56680	No Fancy Hat
115.17592	No Fancy Hat
90.11899	No Fancy Hat
101.75480	No Fancy Hat
91.55890	No Fancy Hat
95.26221	No Fancy Hat
96.45034	No Fancy Hat
88.49243	No Fancy Hat
78.93419	No Fancy Hat
92.24074	No Fancy Hat
105.75134	No Fancy Hat
95.33047	No Fancy Hat
98.06387	No Fancy Hat
78.88911	No Fancy Hat
94.96834	No Fancy Hat
115.46699	No Fancy Hat
97.64931	No Fancy Hat
111.45735	No Fancy Hat
95.34913	No Fancy Hat
114.70564	No Fancy Hat
89.87167	No Fancy Hat
83.54903	No Fancy Hat
103.64673	No Fancy Hat
83.22989	No Fancy Hat
111.46339	No Fancy Hat
99.93894	No Fancy Hat
113.50554	No Fancy Hat
92.86566	No Fancy Hat
104.78422	No Fancy Hat
87.57893	No Fancy Hat
94.41480	No Fancy Hat
82.89052	No Fancy Hat

Und grafisch dargestellt (als Boxplot):

# plot both groups
FancyHat %>% 
    ggplot() +
    geom_boxplot ((aes(y = Creativity, x = Group))) +
    labs(title= "Box Plot of Creativity Values") +
    theme_bw()

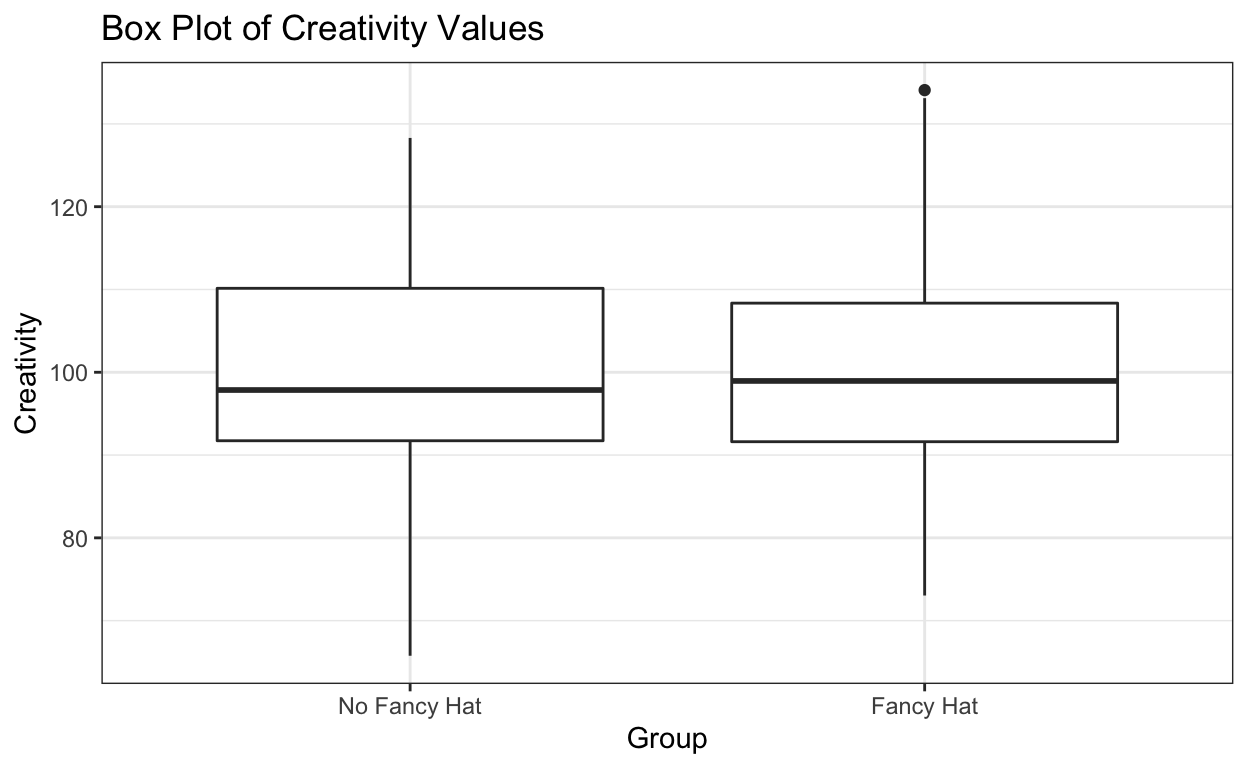
Unter der Annahme, dass die beiden Gruppen dieselbe Standardabweichung haben, machen wir einen t-Test:

fancyhat_ttest <- t.test(Creativity ~ Group,
       var.equal = TRUE,
       data = FancyHat)

fancyhat_ttest_tab <- broom::tidy(fancyhat_ttest)

fancyhat_ttest_tab %>%
    select(estimate, estimate1, estimate2, statistic, p.value, conf.low, conf.high) %>%
    round(3) %>% 
    kbl() %>%
    kable_classic(full_width = FALSE, html_font = "Cambria")

estimate	estimate1	estimate2	statistic	p.value	conf.low	conf.high
-1.647	99.209	100.856	-0.637	0.526	-6.78	3.486

Es ist vielleicht nicht ganz offensichtlich, dass wir hier mehrere Dinge gemacht haben:

Wir haben zwei Mittelwerte geschätzt. Genauer gesagt haben wir zwei Punktschätzungen der Gruppenmittelwerte¹.
Wir schätzen die resultierende Differenz der Gruppenmittelwerte².
Wir berechnen eine Teststatistik (empirischer t-Wert)³.
Wir berechnen die Wahrscheinlichkeit, unter der Nullhypothese einen t-Wert zu erhalten, der einen mindestens so grossen Betrag hat wie der empirische t-Wert⁴.

Diskutieren Sie die Bedeutung des erhalten p-Wertes und des Konfidenzintervalles. Finden Sie diese Konzepte intuitiv verständlich? Können Sie erklären, was ein Konfidenzintervall ist?

Der p-Wert beträgt 0.53. Was können wir damit anfangen?

Weitere Probleme

Es gibt viele weitere Probleme mit dem frequentistischen Ansatz (Wagenmakers 2007)—die oben genannten haben damit zu tun, dass die Konzepte nicht sonderlich intuitiv sind. Wir hätten z.B. gerne die Wahrscheinlichkeit, mit der eine Hypothese wahr/falsch ist.

Ein weiteres Problem ist, dass Anreize in der Forschung oftmals dazu verleiten, frequentistische NHST falsch einzusetzen. Verschiedene bad practices sind unter dem Begriff p-hacking bekannt. Damit kann z.B. gemeint sein, viele Hypothesentests durchzuführen, aber nur diejenigen zu Berichten, welche ein signifikantes Resultat ergeben.

Schlussendlich ist auch so, dass frequentistische Statistik nicht den von den Axiomen der Wahrscheinlichkeitstheorie Gebrauch macht, um Parameter zu schätzen, und die Unsicherheit bei der Schätzung nicht anhand einer Wahrscheinlichkeitsverteilung quantifiziert.

Philosophie der Wahrscheinlichkeit

In der klassischen Statistik wird Wahrscheinlichkeit als relative Häufigkeits eines Ereignisses verstanden. Dies bedeutet, dass nur Ereignisse, welche (unendlich) oft wiederholt werden können, eine Wahrscheinlichkeit haben können.

Somit ist es unmöglich, dass Parameter oder Hypothesen eine Wahrscheinlichkeitsverteilung haben können. Zum Vergleich von frequentistischer und Bayesianischer Auffassung von Wahrscheinlichkeiten gibt es hier und hier mehr Information.

Bayesianische Statistik

Degrees of belief

Wir werden nun mit einem anderen Ansatz arbeiten. Dieser beruht auf den Axiomen der Wahrscheinlichkeitstheorie und der Auffassung von Wahrscheinlichkeit als degree of belief, also vom der Grad persönlichen Überzeugung. Daher wird dieser Ansatz of subjektiv genannt.

Die wichtigste Erkenntnis ist jedenfalls: Wahrscheinlichkeitsverteilungen quantifizieren unseren Wissensstand, oder genauer gesagt, unsere Unsicherheit (uncertainty) über etwas. Dies kann eine Aussage sein, wie z.B. “es wird morgen regnen,” oder ein Parameter in einem statistischen Modell, oder eine Hypothese.

Die in 1 abgebildeten Verteilungen zeigen unsere Unsicherheit über eine Variable \(x\). Wir wissen, dass \(x>0\), und wir vermuten, dass \(x<50\). In einem Fall (violette Verteilung) glauben wir sogar mit einiger Sicherheit, dass \(x<10\).

library(tidyverse)

tibble(x = seq(from = 0, to = 60, by = .1)) %>% 
  tidyr::expand(x, nesting(alpha = c(2, 4), 
                    beta  = c(0.1, 1))) %>% 
  mutate(density = dgamma(x, alpha, beta),
         group   = rep(letters[1:2], times = n() / 2)) %>% 
  
  ggplot(aes(x = x, ymin = 0, ymax = density, 
             group = group, fill = group)) +
  geom_ribbon(size = 0, alpha = 3/4) +
  scale_fill_viridis_d(option = "B", direction = -1, 
                       begin = 1/3, end = 2/3) +
  scale_x_continuous(expand = expansion(mult = c(0, 0.05))) +
  scale_y_continuous(NULL, breaks = NULL) +
  coord_cartesian(xlim = c(0, 50)) +
  theme(panel.grid = element_blank(),
        legend.position = "none")

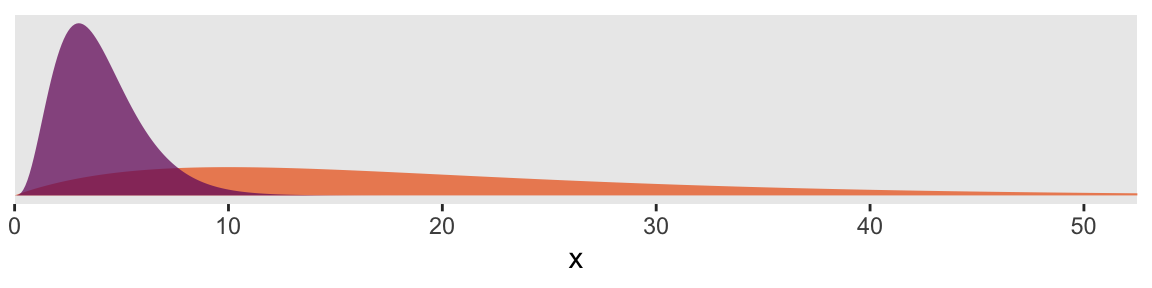
Figure 1: Wahrscheinlichkeitsverteilungen

In der Bayesianischen Statistik erhalten wir anstatt Punktschätzungen von Parametern ganze Verteilungen, mit denen wir unsere Unsicherheit quantifizieren. Ganz stark vereinfacht brauchen wir in der Bayesianischen Statistik eine Prior-Verteilung Englisch: prior), und wir erhalten eine Posteriori-Verteilung (Englisch: posterior), nachdem wir unseren prior anhand der Daten (likelihood) angepasst haben.

Unser prior gibt an, was wir glauben, bevor wir die Daten berücksichtigen, und unser posterior gibt an, was wir glauben, nachdem wir die Daten gesehen haben.

Bayesianische Statistik erfordert also ein paar neue Konzepte, aber längerfristig ist dieser Ansatz einfacher, denn es beruht alles auf ein paar wenigen Grundsätzen.

Die Vorteile des Bayesianischen Ansatzes sind:

intuitiveres Verständnis von Unsicherheit.
erlaubt es uns Evidenz für oder gegen Hypothesen zu quantifizieren.
dieser Ansatz ist viel flexibler.
Wir können unser Wissen in Form von a priori-Verteilungen miteinbeziehen.
besser geeignet für Multilevel Modelle.

Bayesianische Statistik hat aber auch Nachteile:

wir brauchen leistungsstarke Computer.
setzt Familiarität mit Wahrscheinlichkeitsverteilungen voraus.
es ist nicht einfach, Hypothesentests durchzuführen. Siehe z.B. hier und hier.

Warum brauchen wir viel Rechenpower, um Bayesianische Statistik zu machen?

Dies hat damit zu tun, dass es nur in ganz wenigen Fällen einfach ist, posterior Verteilungen zu erhalten. In wenigen Fällen ist es möglich, diese analytisch zu bestimmen, in den den meisten Fällen brauchen wir simulationsbasierte Sampling-Verfahren (Markov Chain Monte Carlo Sampling), um die komplexen Wahrscheinlichkeitsverteilungen zu schätzen. Dies erfordert sehr schnelle Prozessoren, und war deshalb in der Vergangenheit nur auf Supercomputern möglich.

Wir werden nun anhand zweier einfacher Beispiele die Bayesianische Parameterschätzung kennenlernen. Danach werden wir komplexere Beispiele betrachten, und Methoden kennenlernen, mit denen wir Hypothesen testen können. Hypothesentests sind eine Form von Modellvergleichen, und hier gibt es mehrere Möglichkeit.

Grundlagen der Bayesianischen Inferenz

Parameter sind Zufallsvariablen

Parameter sind Zufallsvariablen. Im Gegensatz dazu können Parameter im frequentistischen Ansatz keine Verteilung haben.
Parameter kommen aus Wahrscheinlichkeitsverteilung, welche unser Wissen (Unsicherheit) repräsentieren
Die Prior-Verteilung wird anhand der Likelihood (Daten) updated, um ein Posterior-Verteilung zu erhalten.

Drei Schritte der Bayesianischen Datenanalyse

Im Prinzip folgt Bayesianische Datenanalyse immer den folgenden drei Schritten:

Wir schreiben ein Wahrscheinlichkeitsmodell auf, bestehen aus einer gemeinsamen Verteilung der beobachtent Variablen (\(y\), \(x\)) und der latenten Parameter \(\theta\)).
Wir berechnen die Posterior-Verteilung \(P(θ | y) \sim P(y | \theta) \cdot p(\theta)\), beruhend auf den beobachteten Daten.
Wir evaluieren das Modell und die Posterior-Verteilung.
- Wie gut passt das Modell?
- Sind unsere Schlussfolgerungen gerechtfertigt?
- Wie empfindlich sind unsere Schätzungen gegenüber unseren Annahmen?
- Müssen wir unser Modell revidieren?
- Wir können anhand von Modellvergleichen Hypothesen testen.

Parameterschätzung: Wahrscheinlichkeitsparameter einer Binomialverteilung

Wir schauen uns nun diesen Prozess anhand eines simplen Beispiels an.

Beispiel

Zwei Kartenspieler spielen gegeneinander. Sie beobachten, dass Spielerin A 6 von 9 Spielen gewinnt, während Spielerin B nur 3 davon gewinnt. Sie fragen sich nun, ob das nur Glück ist, oder ob Spielerin A tatsächlich besser sein könnte.

Dieses Beispiel ist analytisch lösbar. Ich werde die analytische Lösung in einem Blog Post demonstrieren, da wir hier eine simulationsbasierte Lösung anstreben.

Wenn Sie diesen Sachverhalt quantifizieren möchten, könnten Sie behaupten, dass die Wahrscheinlichkeit, dass Spielerin A gewinnt, grösser als 0.5 sein müsste, falls diese besser ist. Eine Wahrscheinlichkeit von 0.5 würde bedeuten, dass beide mit gleicher Wahrscheinlichkeit gewinnen.

Unser Ziel ist es also, den Wahrscheinlichkeitsparameter \(\theta\) einer Binomialverteilung zu schätzen. Die Daten, \(y\), sind in diesem Fall die 6 Erfolge in 9 Versuchen.

wins <- 6
games <- 9

Wir wissen, dass die Anzahl Erfolge in k Spielen einer Binomialverteilung folgt. Falls beide Spielerinnen gleich gut sind, sollte die Erfolgswahrscheinlichkeit ungefähr 0.5 sein. Wir können die Wahrscheinlichkeit berechnen, dass Spielerin A durch Glück 6 Spiele gewinnt, d.h. unter der Annahme, dass beide gleich gut sind.

dbinom(x = wins, size = games, prob = 0.5)

[1] 0.1640625

Diese Wahrscheinlichkeit ist ziemlich hoch. Wir können auch die kumulative Wahrscheinlichkeit berechnen, 5 mal oder weniger zu gewinnen:

pbinom(q = 5, size = games, prob = 0.5)

[1] 0.7460937

Die Wahrscheinlichkeit, 6, 7, 8 oder 9 mal zu gewinnen wäre demnach:

1 - pbinom(q = 5, size = games, prob = 0.5)

[1] 0.2539063

oder

pbinom(q = 5, size = games, prob = 0.5, lower.tail = FALSE)

[1] 0.2539063

Wir können aber auch eine Punktschätzung der Wahrscheinlichkeit erhalten.

theta <- wins/games
theta

[1] 0.6666667

Dies entspricht derjenigen Schätzung, für welche die Wahrscheinlichkeit maximiert wird, diese Daten zu beobachten. Dies nennt man eine Maximum Likelihood Schätzung.

tibble(x = seq(from = 0, to = 1, by = .01)) %>% 
  mutate(density = dbinom(6, 9, x)) %>% 
  
  ggplot(aes(x = x, ymin = 0, ymax = density)) +
  geom_ribbon(size = 0, alpha = 1/4, fill = "steelblue") +
  geom_vline(xintercept = theta, linetype = 2, size = 1.2) +
  scale_y_continuous(NULL, breaks = NULL) +
  coord_cartesian(xlim = c(0, 1)) +
  xlab("Wahrscheinlichkeit") +
  theme(panel.grid = element_blank(),
        legend.position = "none")

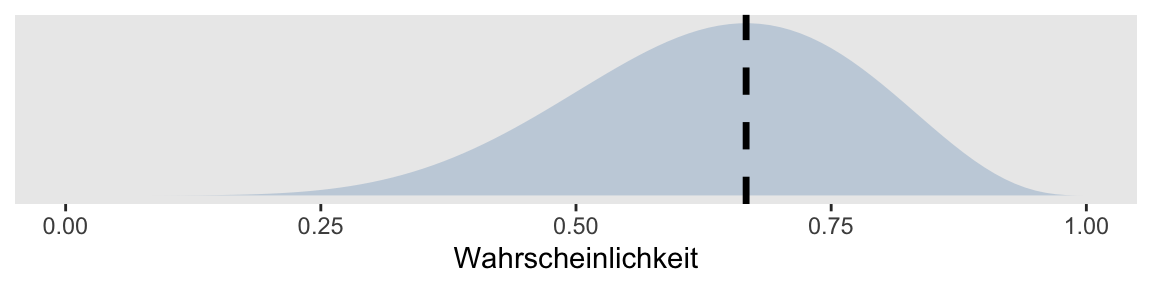
Figure 2: Maximum-Likelihood Schätzung

Grafik 2 zeigt, dass \(\theta\) = 6/9 derjenige Parameter ist, für den die Wahrscheinlichkeit maximiert wird, dass wir 6 Erfolge in 9 Spielen beobachten.

Bayes’ Theorem

Mit einer Punktschätzung können wir unsere Unsicherheit aber nicht quantifizieren—dafür brauchen wir eine Verteilung über den ganzen Bereich der möglichen Parameterwerte. Diese Verteilung erhalten wir, indem wir das Bayes’sche Theorem anwenden. Die Wahrscheinlichkeit, dass A gewinnt, \(\theta\), bedingt auf die Daten, ist:

\[ P(\theta|Data) = \frac{ P(Data|\theta) * P(\theta) } {P(Data)}\] Der Term \(P(Data)\) ist eingentlich nur eine Normalisierungskonstante, welche dafür sorgt, dass wir eine Verteilung erhalten (welche zu 1 integriert), und wird oft weggelassen:

\[ P(\theta|Data) \propto P(Data|\theta) * P(\theta) \] Um dies zu berechnen, brauchen wir \(P(Data|\theta)\) und \(P(\theta)\). \(P(Data|\theta)\) ist einfach; die Wahrscheinlichkeit \(k\) Erfolge in \(n\) Versuchen zu erhalten ist

\[ P(x = k) = {n \choose k} \theta^k (1-\theta)^{n-k} \] Das bedeutet: \(k\) Erfolge mit Wahrscheinlichkeit \(\theta^k\) und \(n-k\) Misserfolge mit Wahrscheinlichkeit \(1-\theta^{n-k}\). Mit dem Term \(\binom{n}{k} = \frac{n!}{k!(n-k)!}\) berücksichtigen wir alle Reihenfolgen, mit denen wir 6 Erfolge in 9 Spielen erhalten.

\(P(\theta)\) ist die a-priori-Wahrscheinlichkeit, mit der Spielerin A gewinnt. Wenn wir nicht über die beiden Spielerinnen wissen, ist es sinnvoll anzunehmen, dass alle Wahrscheinlichkeiten zwischen 0 und 1 gleichwahrscheinlich sind. So eine Verteilung nennt man eine uniforme Verteilung über dem Interval \(\left(0, 1\right) = \{x \in \mathbb{R} | 0 < x < 1 \}\).

Wir definieren nun einen Vektor von möglichen Werten:

n_points <- 100
p_grid <- seq( from=0 , to=1 , length.out = n_points )

Die Likelihood, das heisst die Wahrscheinlichkeit der Daten für jeden möglichen Parameterwert, ist

likelihood <- dbinom(wins , size = games , prob = p_grid)

compute_posterior = function(likelihood, prior){
  # compute product of likelihood and prior
  unstandardized_posterior <- likelihood * prior
  
  # standardize the posterior, so it sums to 1
  posterior <- unstandardized_posterior / sum(unstandardized_posterior)
  
  par(mfrow=c(1, 3))
  plot(p_grid , prior, type="l", main="Prior", col = "dodgerblue3", lwd = 2)
  plot(p_grid , likelihood, type="l", main="Likelihood", col = "firebrick3", lwd = 2)
  plot(p_grid , posterior , type="l", main="Posterior", col = "darkorchid3", lwd = 2)
}

prior1 <- rep(0.5 , length(p_grid))
compute_posterior(likelihood, prior1)

Da wir jeden Wert für gleich wahrscheinlich hielten, hat unser Prior keinen Einfluss auf den Posterior.

Wir können aber unser Vorwissen auch anders ausdrücken. Vielleicht halten wir es für möglich, dass A besser ist als B, aber wir glauben, es sei unmöglich, dass B besser ist. Dieser Glaube könnte durch folgenden Prior repräsentiert werden.

prior2 <- ifelse(p_grid < 0.5, 0, 1)
compute_posterior(likelihood, prior2)

Dies führt dazu, dass in unserem Posterior Werte \(< 0.5\) nicht möglich sind, weil wir dieses Vorwissen in unserem Prior spezifiziert hatten.

Wir können aber auch abenteuerliche Priors benutzen, wie z.B. folgender: Wir glauben, dass \(0.5\) der wahrscheinlichste Wert ist, mit einem exponentiellen Abfall auf beide Seiten.

prior3 <- exp(-10 * abs(p_grid - 0.5))
compute_posterior(likelihood, prior3)

Beta Verteilung

Da wir aber nicht immer unsere Prior Verteilungen per Hand spezifieren können oder wollen, ist es oft ratsam, eine bekannte Wahrscheinlichkeitsverteilung zu benutzen. Diese muss einen Wertebereich haben, der für den zu schätzenden Parameter angemessen ist. In diesem Fall ist dies das Interval \(\left(0, 1\right)\).

Die Familie von Verteilungen, die hier in Frage kommen, sind die Beta-Verteilungen. Diese haben zwei Parameter, \(\alpha\) und \(\beta\), welche als Vorwissen über Erfolge und Misserfolge interpretiert werden können. Die Anzahl Versuche ist somit \(\alpha + \beta\). Diese Familie von Verteilungen kann je Nach Wahl der beiden Parameter unterschiedliche Formen annehmen. In Grafik 3 sind einige dargestellt.

length <- 1e4
d <- crossing(shape1 = c(.1, 1:4),
           shape2 = c(.1, 1:4)) %>%
  tidyr::expand(nesting(shape1, shape2),
         x = seq(from = 0, to = 1, length.out = length)) %>% 
  mutate(a = str_c("a = ", shape1),
         b = str_c("b = ", shape2),
         group = rep(1:length, each = 25))

d %>% 
  ggplot(aes(x = x, group = group)) +
  
  geom_line(aes(y = dbeta(x, shape1 = shape1, shape2 = shape2)),
            color = "steelblue4", size = 1.1) +
  scale_x_continuous(expression(theta), breaks = c(0, .5, 1)) +
  coord_cartesian(ylim = c(0, 3)) +
  labs(title = "Beispiele von Beta Verteilungen",
       y = expression(p(theta*"|"*a*", "*b))) +
  theme(panel.grid = element_blank()) +
  facet_grid(b~a)

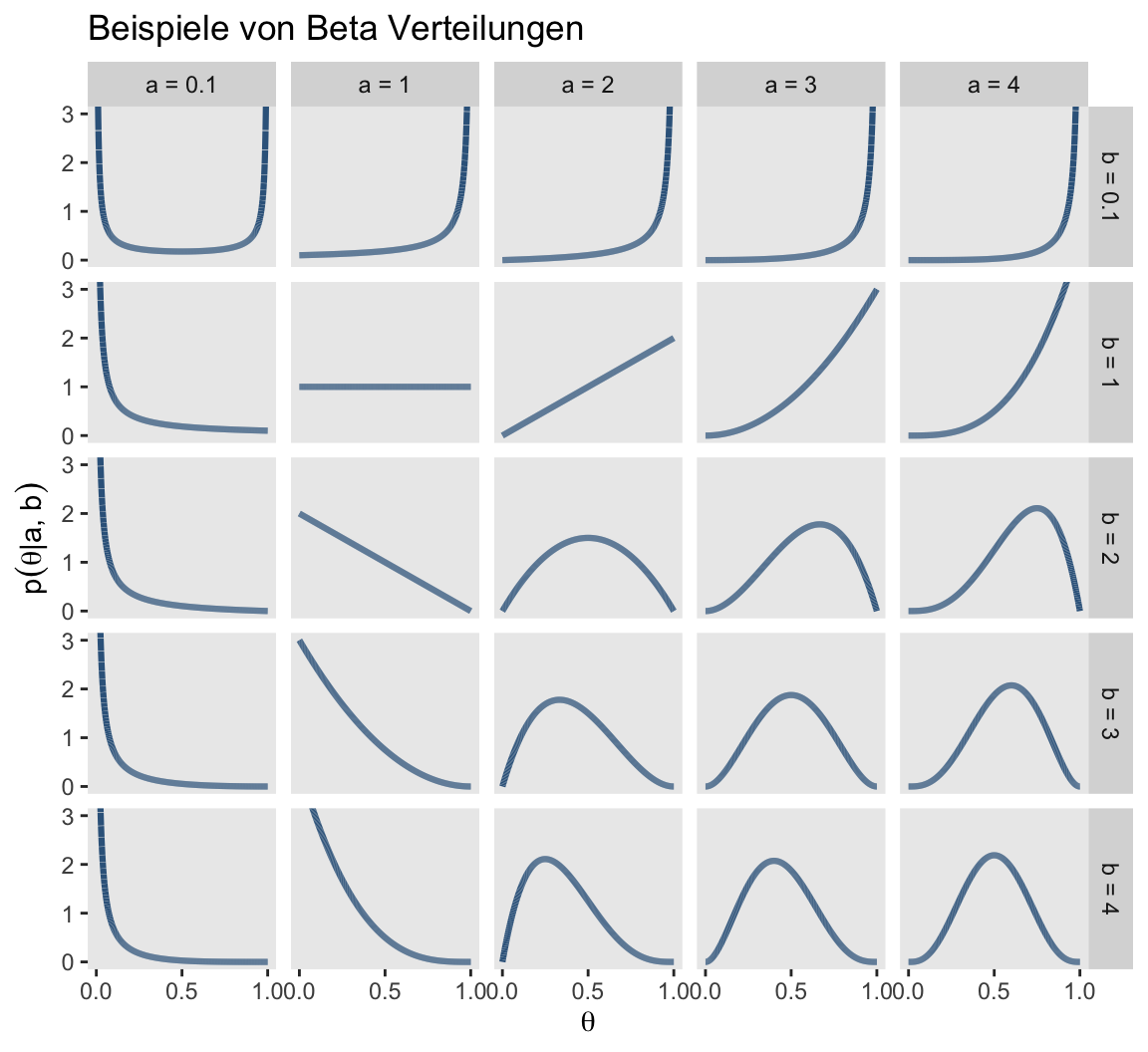
Figure 3: Beta Verteilungen

Die uniforme Verteilung erhalten wir, wenn wir \(\alpha = \beta = 1\) setzen. Wenn wir \(\alpha = \beta = 4\) setzen, erhalten wir eine Verteilung mit Erwartungswert \(0.5\)—dies ist der Fall für alle Verteilungen in denen die beiden Parameter denselben Wert annehmen. Wenn wir ausdrücken wollen, dass wir A für die bessere Spielerin als B halten, dann wählen wir \(\alpha > \beta\).

Die Verteilungsfunktionen heissen in R dbeta(), pbeta(), qbeta() und rbeta(). Die Parameter \(\alpha\) und \(\beta\) heissen ganz einfach shape1 und shape2.

prior4 <- dbeta(x = p_grid, shape1 = 20, shape2 = 4)
compute_posterior(likelihood, prior4)

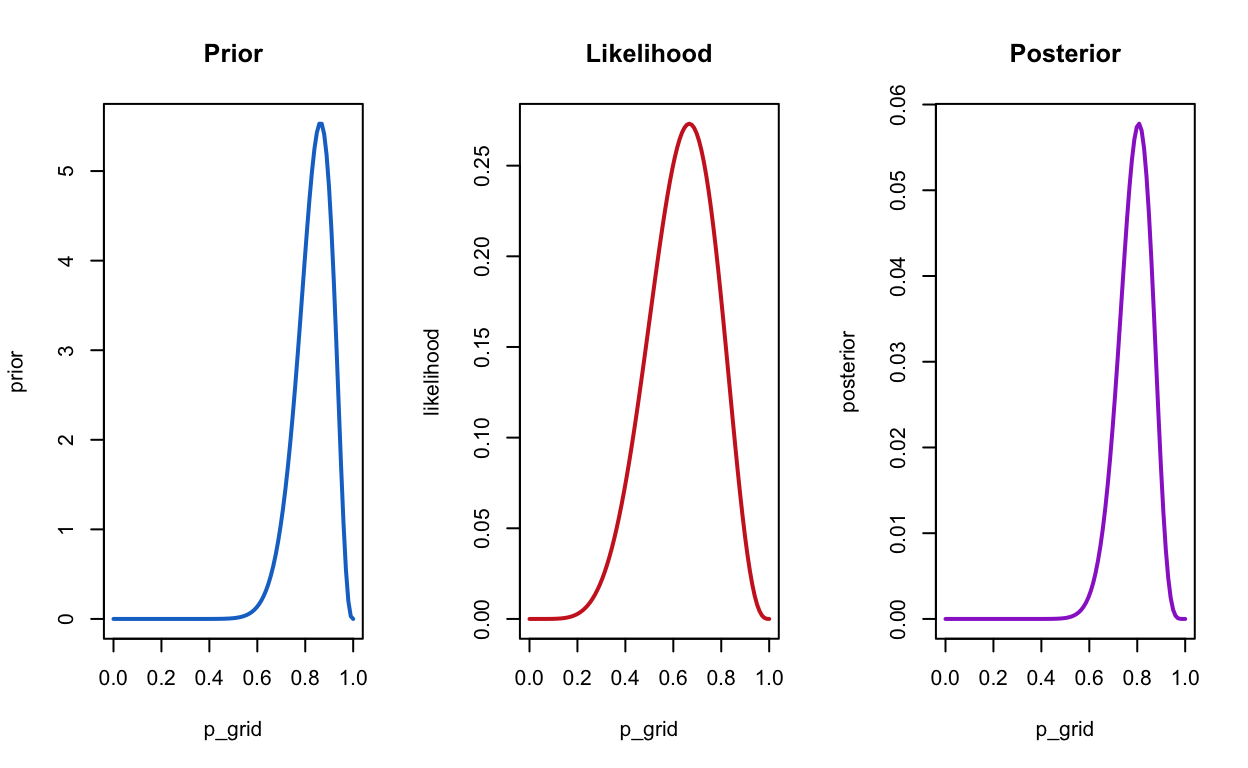
Wenn wir überzeugt wären, dass B besser ist, dann hätten wir vielleicht diesen Prior:

prior5 <- dbeta(x = p_grid, shape1 = 4, shape2 = 20)
compute_posterior(likelihood, prior5)

Einfluss des Priors auf den Posterior

Die obigen Beispiele illustrieren, dass die Prior-Verteilung einen grossen Einfluss auf die Schätzung haben kann. Deshalb ist bei der Wahl der Prior Vorsichtig geboten; vor allem wenn es darum geht, Parameter in statistischen Modellen zu schätzen, wollen wir oft sogenannte non-informative Priors, welche keine nennenswerten Einfluss auf die Schätzung haben.

Schätzmethoden

Die Methode, welche wir oben angewandt haben, nennt sich “grid approximation.” Dies bezieht sich auf den Prior—wir haben einen Vektor von Priorwerten definiert, und jeden Punkt mit der Likelihood multipliziert, in direkter Anwendung von Bayes’ Theorem. Dies ist für dieses kleine Problem sehr gut möglich. Daneben gibt es für dieses Beispiel auch die analytische Lösung. Die Beta-Prior-Verteilung kann mit den beobachteten Erfolgen und Versuchen updated werden, um eine neue Beta-Verteilung mit den Parametern \(k + \alpha\) und \(n - k + \beta\).

Nun kommen diese beiden Ansatz für die meisten Datenanalyseprobleme nicht in Frage. Die analytische Lösung ist nicht möglich, und die grid-search Methode ist nicht in endlicher Zeit durchführbar. In diesem Fall sind wir auf approximative Methoden angewiesen. Eine Variante, welche die Posterior-Verteilung durch Ziehen von Zufallszahlen exploriert, heisst Markov CHain Monte Carlo. Davon gibt es wiederum verschiedene Varianten.

Stan

Ein Algorithmus, welcher als state-of-the-art gilt, heisst Hamiltonian Monte Carlo, und eine spezielle Variante davon heisst NUTS (No-U-Turn Sampler). Auf diese Inferenzmethode ist die probabilistische Programmiersprache Stan spezialisiert.

Wir werden in dieser Veranstaltung selten Stan direkt verwenden, da es mittlerweile gute R Packages gibt, mit denen die Bedienung von Stan sehr einfach geworden ist. Ich halte es jedoch für pädagogisch wertvoll, wenn wir uns zumindest dieses Beta-Binomial Besipiel in Stan anschauen.

Die Vorgehensweise ist genauso, wie oben beschrieben: wir schreiben zuerst ein probabilistischen Model⁵ auf, und bedingen dann auf die beobachteten Daten.

Das Modell wird in der Stan Sprache geschrieben. Wir verwenden hier einen Beta(4, 4) Prior.

data {
  int<lower=0> n; // number of games
  int<lower=0> k; // number of wins
  
}

parameters {
  real<lower=0, upper=1> theta;
}

model {
  theta ~ beta(4, 4);
  k ~ binomial(n, theta);
}

Dieser Code wird in einem File mit dem Suffix .stan gespeichert.

Ich nenne das Stan File binomial-model.stan.

Wir laden das Package rstan, das R Interface zu Stan.

library(rstan)

Dann definieren wir die beobachteten Daten:

stan_data <- list(
  n = 9,
  k = 6
)

Und benutzen die Funktion stan(), um die Posterior-Verteilung zu sampeln.

fit <- stan(file = "binomial-model.stan",  # Stan program
            data = stan_data,    # named list of data
            chains = 4,          # number of Markov chains
            iter = 2000,         # total number of iterations per chain
            cores = 4)           # number of cores (could use one per chain)

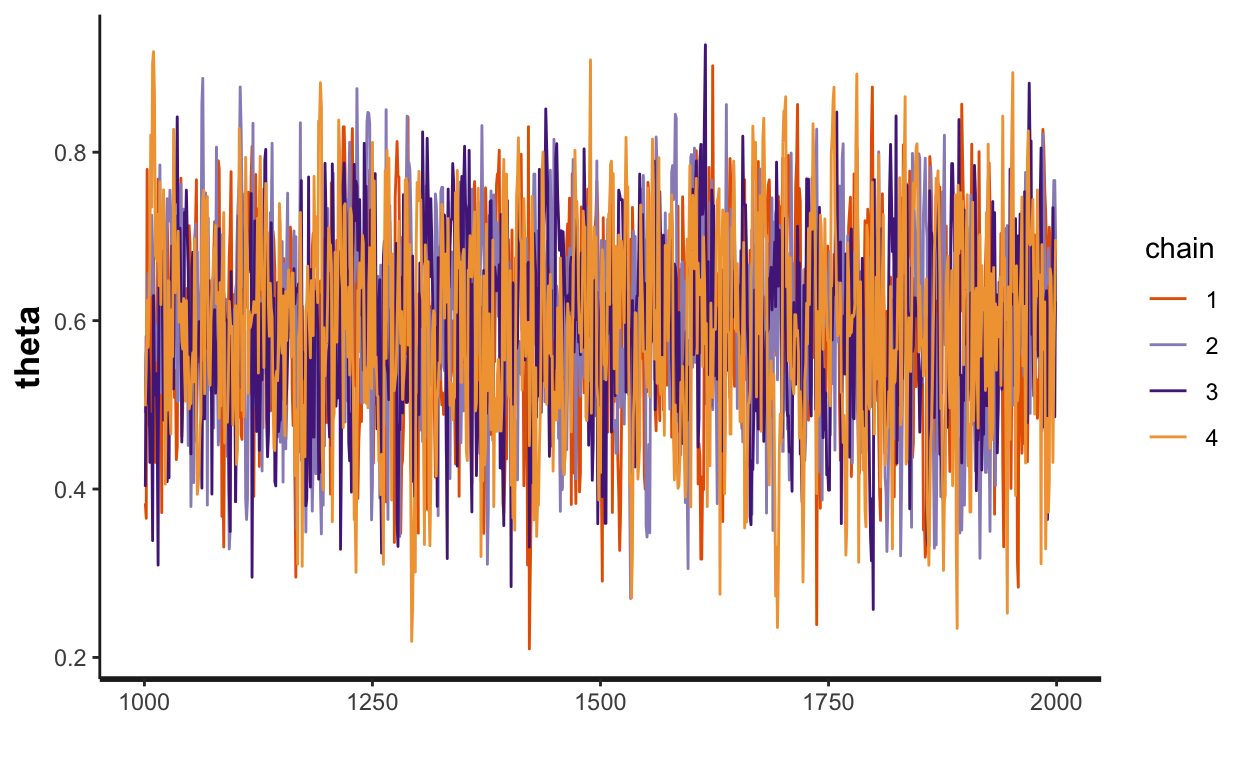
print(fit)

Inference for Stan model: binomial-model.
4 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=4000.

        mean se_mean   sd   2.5%    25%    50%    75%  97.5% n_eff
theta   0.59    0.00 0.12   0.36   0.51   0.60   0.68   0.80  1497
lp__  -12.04    0.02 0.74 -14.11 -12.22 -11.75 -11.57 -11.52  1976
      Rhat
theta    1
lp__     1

Samples were drawn using NUTS(diag_e) at Sat Mar 13 01:36:41 2021.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

traceplot(fit)

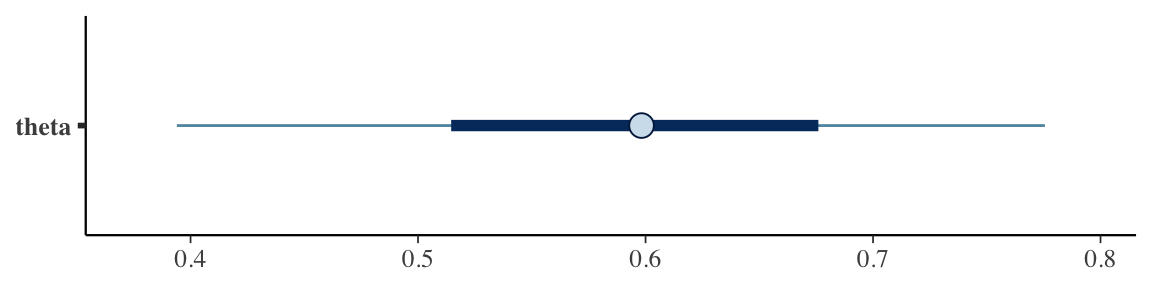
bayesplot::mcmc_intervals(fit, "theta")

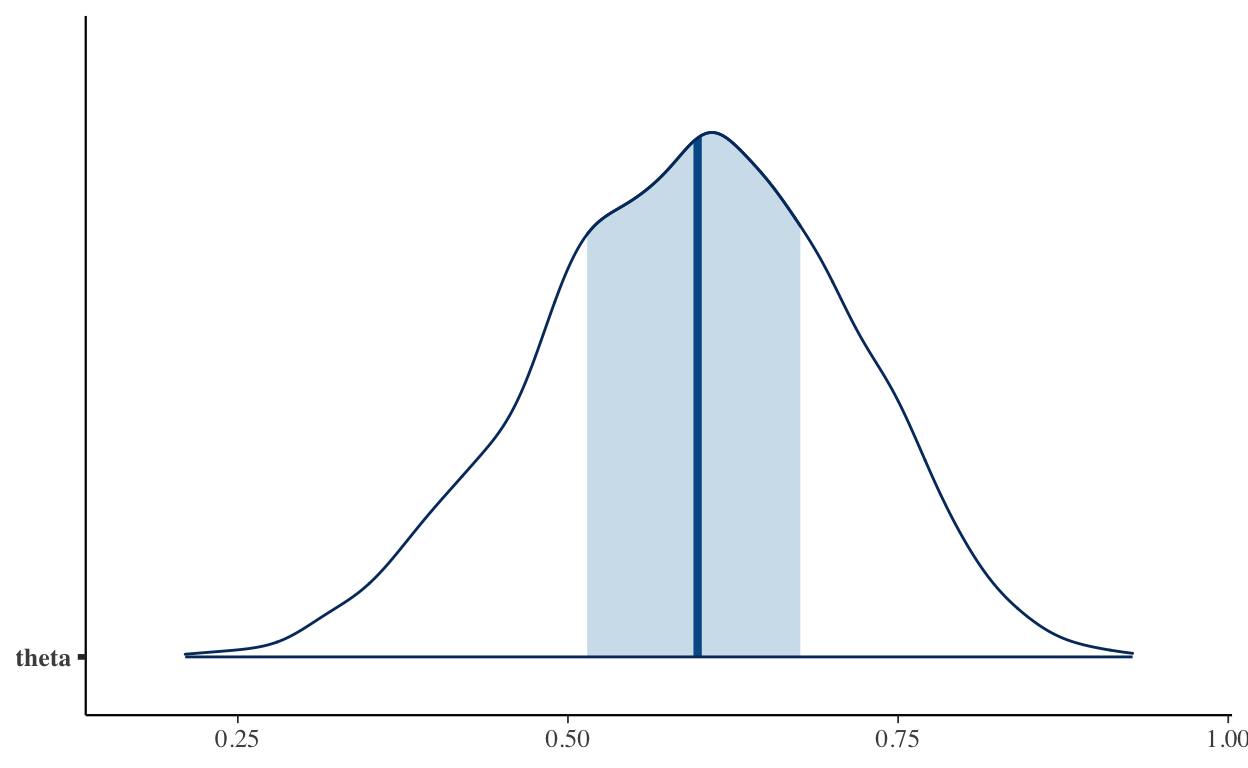
bayesplot::mcmc_areas(fit, "theta")

brms

library(brms)

data <- tibble(k = 6, n = 9)

priors <- prior(beta(4, 4), class = b, lb = 0, ub = 1)

m1 <- brm(k | trials(n) ~ 0 + Intercept, family = binomial(link = "identity"),
          prior = priors,
          data = data,
          control = list(adapt_delta = 0.9),
          file = "models/binomial-2")

plot(m1)

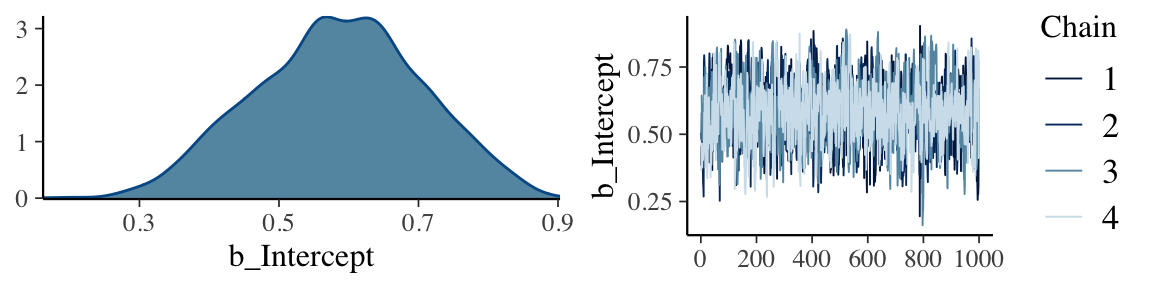
Posterior-Verteilungen zusammenfassen

Wir erhalten mit Bayesianischer Inferenz zwar Posterior-Verteilungen, aber oftmals wollen wir diese zusammen, damit wir eine Entscheidung fällen können.

Dies wird häufig anhand bestimmter Kennzahlen gemacht. Z.B. können wir den Mittelwert oder Median und eine Ober- und Untergrenze wählen. Ein solches Interval wird credible interval genannt. Häufig wird ein \(95\%\) credible interval angegeben, aber es hindert uns nichts daran, ein \(50\%\) oder \(80\%\) credible interval zu benutzen. Mit der median_qi() vom Package tidybayes können wir das .width Argument benutzen:

library(tidybayes)

m1 %>%
  spread_draws(b_Intercept) %>% 
  median_qi(.width = c(.50, .80, .95)) %>% 
  kableExtra::kbl()

b_Intercept	.lower	.upper	.width	.point	.interval
0.5885875	0.5025237	0.6682483	0.50	median	qi
0.5885875	0.4231849	0.7428155	0.80	median	qi
0.5885875	0.3514341	0.8102628	0.95	median	qi

Mit mean_qi() erhalten wir Mittelwert und credible intervals.

Um die Posterior-Verteilung zu visualisieren, können wir die Verteilung mit einem credible interval kombinieren.

m1 %>%
  spread_draws(b_Intercept) %>%
  ggplot(aes(x = b_Intercept)) +
  stat_halfeye(.width = c(.50, .80, .95))

Was ist der Unterschied zwischen einem Konfidenzintervall und einem credible interval? Welches Intervall würden Sie verwenden, um eine Wahrscheinlichkeitsaussage über einen Parameter zu machen?

Weiterführende Literatur

Etz and Vandekerckhove (2018) bieten eine sehr gründliche Einführung, mit vielen (Harry Potter-themed) Beispielen. Schoot et al. (2014) ist ebenfalls eine sehr gründliche Einführung. Eine empfehlenswerte Übersicht über Literatur, vor allem in Bezug auf Psychologie, geben Etz et al. (2016).

Das Buch von (Kruschke 2015) ist ein gutes Lehrbuch, obwohl der R Code nicht unbedingt sehr benutzerfreundlich ist.

Mein Favorit ist McElreath (2020).

Etz, Alexander, Quentin Frederik Gronau, Fabian Dablander, Peter Edelsbrunner, and Beth Baribault. 2016. “How to Become a Bayesian in Eight Easy Steps: An Annotated Reading List,” August. https://doi.org/10.31234/osf.io/ph6sw.

Etz, Alexander, and Joachim Vandekerckhove. 2018. “Introduction to Bayesian Inference for Psychology.” Psychonomic Bulletin & Review 25 (1): 5–34. https://doi.org/10.3758/s13423-017-1262-3.

Gigerenzer, Gerd. 2004. “Mindless Statistics.” The Journal of Socio-Economics 33 (5): 587–606. https://doi.org/10.1016/j.socec.2004.09.033.

———. 2018. “Statistical Rituals: The Replication Delusion and How We Got There.” Advances in Methods and Practices in Psychological Science 1 (2): 198–218. https://doi.org/10.1177/2515245918771329.

Hoekstra, Rink, Richard D. Morey, Jeffrey N. Rouder, and Eric-Jan Wagenmakers. 2014. “Robust Misinterpretation of Confidence Intervals.” Psychonomic Bulletin & Review 21 (5): 1157–64. https://doi.org/10.3758/s13423-013-0572-3.

Kruschke, John. 2015. Doing Bayesian Data Analysis (Second Edition). Boston: Academic Press.

McElreath, R. 2020. Statistical Rethinking: A Bayesian Course with Examples in r and Stan. A Chapman & Hall Book. CRC Press. https://books.google.ch/books?id=Ie2vxQEACAAJ.

Schoot, Rens van de, David Kaplan, Jaap Denissen, Jens B. Asendorpf, Franz J. Neyer, and Marcel A. G. van Aken. 2014. “A Gentle Introduction to Bayesian Analysis: Applications to Developmental Research.” Child Development 85 (3): 842–60. https://doi.org/10.1111/cdev.12169.

Wagenmakers, Eric-Jan. 2007. “A Practical Solution to the Pervasive Problems of p Values.” Psychonomic Bulletin & Review 14 (5): 779–804. https://doi.org/10.3758/BF03194105.

Wasserstein, Ronald L., and Nicole A. Lazar. 2016. “The ASA Statement on p-Values: Context, Process, and Purpose.” The American Statistician 70 (2): 129–33. https://doi.org/10.1080/00031305.2016.1154108.

estimate1 und estimate2↩︎
estimate↩︎
statistic↩︎
p.value↩︎
Dies nennt man ein generatives Modell↩︎

Einführung