Aufgabenstellung
Sie haben für diese Übung eine Woche Zeit. Laden Sie Ihre Lösung als Rmarkdown File bis Donnerstag, 11. März um 00:00 Uhr, in den Order für Übung 1 auf ILIAS. Falls Rmarkdown nicht funkionieren sollte, werden auch Lösungen in Form eines R Skriptes akzeptiert. Nennen Sie Ihr File Matrikelnummer_Nachname_uebung-1.Rmd oder Matrikelnummer_Nachname_uebung-1.R, z. B. 15-172-874_Nachname_uebung-1.Rmd.
Bevor Sie einreichen, vergewissern Sie sich bitte, dass Ihr Rmarkdown File geknittet werden kann, und dass der R Code ohne Fehler läuft.
Sie verabreichen einen Test, der aus 10 Fragen besteht. Die Fragen sind etwa gleich schwierig, und Sie sind sich sicher, dass die Fragen weder zu leicht noch zu schwierig für Ihre Schüler sind. Beim Betrachten der Resultate fällt Ihnen das Ergebnis eines Schülers besonders auf.
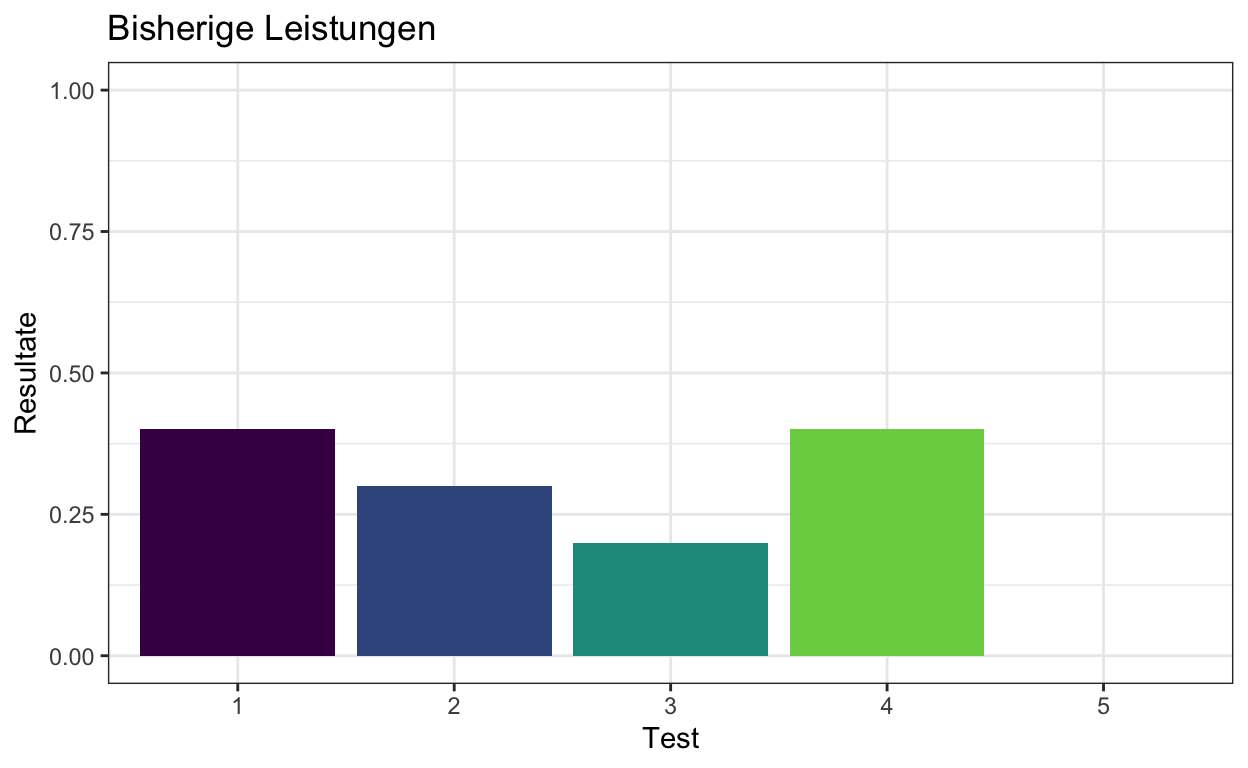
Bisher hatten Sie 4 solcher Tests verabreicht. Dieser Schüler schneidet normalerweise unterdurchschnittlich ab, mit Ergebnissen von \(4/10\), \(3/10\), \(2/10\) und \(4/10\) richtigen Antworten. Sie haben sich schon vorgenommen, die Elter des Schülers zu kontaktieren, da Sie sich Sorgen machen.
tibble(Test = as_factor(1:5), Resultate = c(4/10, 3/10, 2/10, 4/10, NA)) %>%
ggplot(aes(Test, Resultate, fill = Test)) +
geom_bar(stat = 'identity') +
scale_fill_viridis_d(end = 0.8) +
scale_y_continuous(limits = c(0, 1)) +
theme_bw() +
theme(legend.position = "none") +
ggtitle("Bisherige Leistungen")
Bei diesem Test sehen die Antworten aber so aus:
answers <- c(1, 1, 1, 1, 0, 1, 1, 1, 1, 1)
Berechnen Sie die Anzahl korrekter Antworten, sowie die Anzahl korrekter Antworten in den bisherigen Tests.
Sie freuen sich—vielleicht hat sich der Schüler bei diesem Test besonders Mühe gegeben. Sie überlegen sich, ob Sie nun warten sollen, oder doch mit den Eltern einen Termin für ein Gespräch abmachen sollen.
Vielleicht kann Ihnen Bayesianische Inferenz helfen?
Aufgaben
Versuchen Sie, mit Hilfe Ihres Vorwissens über die Leistungen des Schülers seine Fähigkeit (ability), Fragen richtig zu beantworten, zu schätzen. Da Sie wissen, dass Sie die Fähigkeit nur ungenau schätzen können, wollen Sie Ihre Unsicherheit mit einer Posterior Distribution quantifizieren.
Der R Code, den Sie bei dieser Übung brauchen, ist schon gegeben. Sie brauchen lediglich die Lücken auszufüllen.
Zum Beispiel:
ncorrect <- sum(___)wird zu
ncorrect <- sum(answers)
Definieren sie zuerst einen Vektor, der alle möglichen Werte des Parameters \(\theta\) enthält.
n_points <- 100
theta_grid <- seq(from = 0 , to = 1 , length.out = n_points)
Aufgabe 1
Berechnen Sie nun die Wahrscheinlichkeit, das Testergebnis des Schülers zu erreichen, d.h. die Wahrscheinlichkeit der Daten für jeden möglichen Parameterwert.
likelihood <- dbinom(x = ___ , size = ___ , prob = theta_grid)Sie können diese Wahrscheinlichkeit so graphisch darstellen.
tibble(theta_grid, likelihood) %>%
ggplot(aes(x = theta_grid, y = likelihood)) +
geom_line()
Aufgabe 2
Wenn Sie kein Vorwissen über die bisherigen Testresultate des Schülers hätten: Was würden Sie als Schätzung der Fähigkeit des Schülers benutzen?
Aufgabe 3
Versuchen Sie nun, Ihr Vorwissen über die Leistungen des Schülers in Form einer Prior-Verteilung auszudrücken.
prior <- dbeta(x = theta_grid, shape1 = ___, shape2 = ___)Aufgabe 4
Berechnen Sie die Posterior-Verteilung als Produkt von Likelihood und Ihrem Prior.
unstandardized_posterior <- likelihood * prior
posterior <- unstandardized_posterior / sum(unstandardized_posterior)
posterior
Aufgabe 5
Stellen Sie Prior, Likelihood und Posterior grafisch dar
df <- tibble(theta_grid, prior, likelihood, posterior)
df %>%
pivot_longer(-theta_grid, names_to = "distribution", values_to = "density") %>%
mutate(distribution = as_factor(distribution)) %>%
ggplot(aes(theta_grid, density, color = distribution)) +
geom_line(size = 1.5) +
geom_vline(xintercept = 9/10, linetype = "dashed") +
scale_color_viridis_d(end = 0.8) +
xlab("Theta Werte") +
ylab("") +
facet_wrap(~distribution, scales = "free_y") +
theme_bw()
Aufgabe 6
Was ist die Warscheinlichkeit, dass jemand mit solchen Vorleistungen mindestens 9 Fragen von 10 beantwortet, falls die Vorleistungen tatsächlich die wahre Fähigkeiten der Schüler messen?