Übung 2

Parameterschätzung, Posterior zusammenfassen, und lineare Modelle.

true
2021-06-22

Die Aufgaben, die Sie bearbeiten sollen, finden Sie in einem gelben Kasten. Optionale Aufgaben sind in orangen Kästen.

Sie haben für diese Übung 10 Tage Zeit. Laden Sie Ihre Lösung als Rmarkdown File bis Sonntag, 4. April um 00:00 Uhr, in den Order für Übung 2 auf ILIAS. Falls Rmarkdown nicht funkionieren sollte, werden auch Lösungen in Form eines R Skriptes akzeptiert. Nennen Sie Ihr File Matrikelnummer_Nachname_uebung-2.Rmd oder Matrikelnummer_Nachname_uebung-2.R, z. B. 15-172-874_Nachname_uebung-2.Rmd.

Bevor Sie einreichen, vergewissern Sie sich bitte, dass Ihr Rmarkdown File geknittet werden kann, und dass der R Code ohne Fehler läuft.

Aufgabe 1

In der ersten Aufgabe untersuchen Sie einen Datensatz einer Studie, bei der die Arbeitsgedächtnisleitung mittels eines N-Back Tasks bei \(21\) Kindern mit einer ADHS Diagnose untersucht wurde. Gleichzeitig wurde derselbe Task mit einer Kontrollgruppe (\(n=30\)) durchgeführt. Die behavioralen Resultate wurde parallel zu einer fMRI Untersuchung erhoben, damit im Antwortverhalten der Kinder ein Unterschied zur Kontrollgruppe gezeigt werden konnte.

Bei einem N-Back Test wird den Versuchspersonen eine Serie von Stimuli dargeboten (z.B. Buchstaben), und man muss mit einem Tastendruck reagieren, wenn der aktuelle Stimulus gleich dem N-letzten Stimulus war.

Hier sehen Sie ein Beispiel für einen 3-Back Test. Bei den gelb markierten Buchstaben muss die Versuchsperson reagieren.


T A A F A G H R Y Z R V D …

Bei diesem Task untersuchen wir die Reaktionszeiten der Versuchspersonen bei korrekten Antworten. Im Datensatz erhalten Sie die gemittelten Reaktionszeiten der Kinder in der ADHD und der Control Gruppe.

Daten vorbereiten

Laden Sie zuerst die Daten:

library(tidyverse)

nback1 <- read_csv("https://raw.githubusercontent.com/kogpsy/neuroscicomplab/main/data/adhd-nback.csv")

glimpse(nback1)

Rows: 51
Columns: 2
$ rt    <dbl> 1.0267571, 2.0671470, 1.6728257, 1.0355146, 1.0310874,…
$ group <chr> "adhd", "adhd", "adhd", "adhd", "adhd", "adhd", "adhd"…

Konvertieren Sie die Gruppierungsvariable group zu einem Faktor:

nback1 <- nback1 %>% 
  mutate(group = as_factor(group))

Verändern Sie die Reihenfolgen der Faktorstufen:

levels(nback1$group)

NULL
nback1 <- nback1 %>% 
  mutate(group = fct_relevel(group, "control"))

levels(nback1$group)

[1] "control" "adhd"

Einen kurzen Blick auf die Daten werfen:

glimpse(nback1)

Rows: 51
Columns: 2
$ rt    <dbl> 1.0267571, 2.0671470, 1.6728257, 1.0355146, 1.0310874,…
$ group <fct> adhd, adhd, adhd, adhd, adhd, adhd, adhd, adhd, adhd, …

Aufgabe 1.1

Berechnen Sie Mittelwerte und SD pro Gruppe.

nback1 %>% 
  group_by(group) %>% 
  summarise(___,
            ---)

Daten visualisieren

Aufgabe 1.2

Stellen Sie die Daten mit grafisch dar, zum Beispiel mit Histogrammen, Boxplots oder Violin Plots.

Sie sollte ungefähr solche Grafiken erhalten:

Vielleicht hilft Ihnen folgender Code Block:

nback1 %>% 
  ggplot(aes(rt)) +
  geom_histogram(bins = 15) +
  facet_wrap(~group) +
  theme_bw(base_size = 14)

Frequentistische Analyse

Aufgabe 1.3

Mit welcher Methode würden Sie diese Daten analysieren? Beschreiben Sie Ihre Wahl in 1-2 Sätzen und führen Sie einen Test durch. Was können Sie damit aussagen?

Bayesianische Analyse

Wir wollen nun die beiden Gruppenmittelwerte Bayesianisch schätzen. Sie haben zwei Möglichkeiten kennengelernt, die Formel zu spezifieren.

Aufgabe 1.4

Entscheiden Sie sich für eine der beiden, und schätzen sie die Mittelwerte mit brms. Schauen Sie sich vorher mit der Funktion get_prior die Default Prior Verteilungen an. Wenn sie wollen, können Sie anstelle der Defaults eigene Priors spezifieren. Falls Sie das tun, begründen Sie kurz Ihre Wahl.

library(brms)

get_prior(rt ~ ___,
          data = nback1)

Aufgabe 1.5

Schätzen Sie nun die Parameter Ihres Modells.

library(brms)
m1 <- brm(___ ~ ___,
          data = nback1,
          file = "nback1")

Optionale Aufgabe: fassen Sie die Posterior Verteilung des/der relevanten Parameter(s) mit Hilfe der Funtion mean_qi() im tidybayes Packages zusammen.

Grafische Darstellung

Anstatt sich nur eine Tabelle anzuschauen, ist es hilfreich, die Verteilungen grafisch darzustellen.

Aufgabe 1.6

Stellen Sie die Posterior Verteilung(en) grafisch dar. Sie können dies entweder mit der Funktion mcmc_plots() im brms Package, oder (optional) mit dem tidybayes Package machen. Eine Anleitung für das tidybayes Package finden Sie im 3. Kapitel des Skripts.

m1 %>% 
  mcmc_plot(___)

Diskussion

Aufgabe 1.7

Aufgabe 2

In der zweiten Aufgabe untersuchen Sie einen Datensatz einer Studie, bei der die Arbeitsgedächtnisleitung mittels eines N-Back Tasks bei 20 gesunden Erwachsenen unter verschiedenen Cognitive Loads untersucht wurde. Ziel dieser Studie war es, die Auswirkung von Cognitive Load auf den Präfrontalen Cortex mittels fMRI zu untersuchen. Wir erwarten, dass bei höherem Cognitive Load die Versuchspersonen länger brauchen, um beim N-Back Task eine korrekte Antwort zu geben.

Daten vorbereiten

Wir laden die Daten:

library(tidyverse)
library(rmarkdown)

nback2 <- read_csv("https://raw.githubusercontent.com/kogpsy/neuroscicomplab/main/data/cognitive-load-nback.csv") %>% 
  mutate(across(-rt, as_factor))
nback2 %>% paged_table()

Wir haben 20 Personen

nback2 %>% 
  summarize(n_subjects = n_distinct(id))

# A tibble: 1 x 1
  n_subjects
       <int>
1         20

mit 60 Trials pro Person pro Bedingung. Für jeden Trial haben wir die Reaktionszeit in Millisekunden.

nback2 %>% 
  group_by(id, load) %>% 
  count() %>% 
  rmarkdown::paged_table()

Daten zusammenfassen

Da die Standardfehler Funktion in R nicht existiert, schreiben wir selber eine:

se <- function(x) sd(x)/sqrt(length(x))

Aufgabe 2.1

Fassen Sie die Daten mit Mittelwert, Standardabweichung und Standardfehler pro Person pro Bedingung zusammen.

Aufgabe 2.2

Sie haben die Kennzahlen für jede Person berechnet. Meistens wollen wir aber nicht nur die Effekte der experimentellen Manipulationen für Individuen, sondern für die ganze Gruppe.

Berechnen Sie die mittlere RT für die beiden Bedingungen, aggregiert über Personen. Wie würden Sie vorgehen? Überlegen Sie sich, was die Vor- und Nachteile eines solches Vorgehens sind, und beschreiben Sie sie kurz.

Daten visualisieren

Auch hier ist es sinnvoll, die Daten zuerst grafisch darzustellen.

Aufgabe 2.3

Stellen Sie die mittleren RTs für jede Bedingung aggregiert über Personen grafisch dar.

Sie brauchen wahrscheinlich folgenden Code:

aggregated <- nback2 %>% 
  group_by(id, load) %>% 
  summarise(rt = mean(rt)) %>% 
  group_by(load) %>% 
  summarise(mean = mean(rt))

aggregated %>% 
  ggplot(aes(load, mean)) +
  geom_line(aes(group = 1), linetype = 3) +
  geom_point(size = 4) +
  theme_bw()

Frequentistische Analyse

Aufgabe 2.4

Überlegen Sie sich, wie Sie diesen Datensatz frequentistisch analysieren könnten. Beschreiben Sie in 1-2 Sätzen, was Sie tun würden, und welche Aussagen Sie damit machen könnten.

Bayesianische Analyse

Wir wollen nun die population-level Effects mit brms schätzen, und zwar die Mittelwerte der beiden Cognitive Load Bedingungen. Dafür benutzen wir die Formel ~ 0 + load.

Wir erhalten folgende Default Priors:

get_prior(rt ~ 0 + load + (1 | id),
          data = nback2)

                 prior class      coef group resp dpar nlpar bound
                (flat)     b                                      
                (flat)     b    loadhi                            
                (flat)     b    loadlo                            
 student_t(3, 0, 94.1)    sd                                      
 student_t(3, 0, 94.1)    sd              id                      
 student_t(3, 0, 94.1)    sd Intercept    id                      
 student_t(3, 0, 94.1) sigma                                      
       source
      default
 (vectorized)
 (vectorized)
      default
 (vectorized)
 (vectorized)
      default

Die beiden flachen Priors der Parameter loadhi und loadlo wollen wir nun durch eigene Priors ersetzen. Wir nehmen hier einfach Normalverteilungen, mit einem Mittelwert, der dem Gesamtmittelwert entspricht, und einer etwas arbiträr gewählten Standardabweichung von \(10\).

grandmean <- round(mean(nback2$rt), 0)
grandmean

[1] 822

Priors können mit set_prior() oder einfach nur prior() definiert werden.

priors <- set_prior("normal(822, 10)", class = "b")
# oder
priors <- prior(normal(822, 10), class = b)

Wir schätzen das Model nun mit unseren Prior Verteilungen.

m2 <- brm(rt ~ 0 + load + (1 | id),
          prior = priors,
          data = nback2,
          file = "nback2")

Posterior zusammenfassen und Grafische Darstellung

Aufgabe 2.5

Überprüfen Sie, ob die Rhat Werte in Ordnung sind. Falls ja, fassen Sie die Posterior Verteilung der wichtigen Parameter zusammen. Stellen Sie die Posterior Verteilungen der beiden Bedingungsparameter grafisch dar, z.B. mit mcmc_plot().

Falls Sie die Verteilung der Differenz wollen, können Sie entweder das Modell so parametrisieren: ~ 1 + load + (1 | id), oder die Differenz nachträglich für jede Iteration berechnen. Dies können Sie so machen.

samples_m2 <- posterior_samples(m2) %>% 
    transmute(hi = b_loadhi,
              lo = b_loadlo, 
              diff = hi - lo)

Diese Differenz können Sie jetzt auch zusammenfassen

library(tidybayes)

samples_m2 %>% 
  select(diff) %>% 
  median_qi()

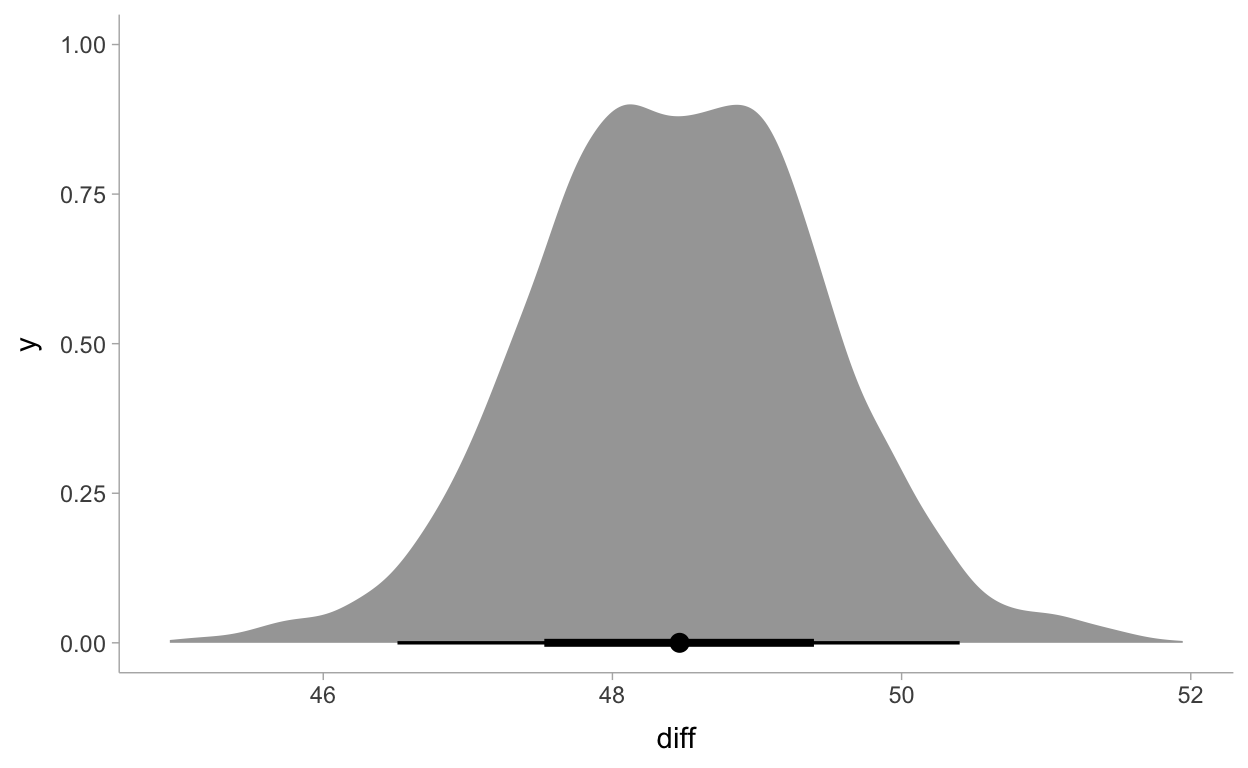
      diff   .lower  .upper .width .point .interval
1 48.46462 46.51335 50.4016   0.95 median        qi

und grafisch darstellen.

samples_m2 %>% 
  select(diff) %>% 
  ggplot(aes(x = diff)) +
  stat_halfeye(point_interval = median_qi) +
  theme_tidybayes()

Diskussion

Aufgabe 2.6

Meule, Adrian. 2017. “Reporting and Interpreting Working Memory Performance in n-Back Tasks.” Frontiers in Psychology 8. https://doi.org/10.3389/fpsyg.2017.00352.

References

Corrections

If you see mistakes or want to suggest changes, please create an issue on the source repository.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY 4.0. Source code is available at https://github.com/kogpsy/neuroscicomplab, unless otherwise noted. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".

Citation

For attribution, please cite this work as

Ellis (2021, June 22). neuroscicomplab: Übung 2. Retrieved from https://kogpsy.github.io/neuroscicomplab/exercise-2.html

BibTeX citation

@misc{ellis2021übung,
  author = {Ellis, Andrew},
  title = {neuroscicomplab: Übung 2},
  url = {https://kogpsy.github.io/neuroscicomplab/exercise-2.html},
  year = {2021}
}

© Copyright 2021 Andrew Ellis

Software licensed under the Creative Commons Zero v4.0 Universal.