neuroscicomplab: Datenanalyse

Andrew Ellis

Logistische Regression

Wir untersuchen die Logistische Regression anhand eines Beispiels aus dem Online Buch Bayesian Data Analysis for Cognitive Science. Wir gehen hier der Frage nach ob die Anzahl Stimuli (Wortlisten unterschiedlicher Länge) einen Einfluss auf die Working Memory Kapazität hat.

Die Daten stammen aus Oberauer (2019). Versuchspersonen wurden Wortlisten mit 2, 4, 6, oder 8 Elementen gezeigt (set_size), und sie mussten danach Wörter anhand ihrer Position wiedergeben.

Ein Trial dieses Experiments ist in Figure 1 dargestellt.

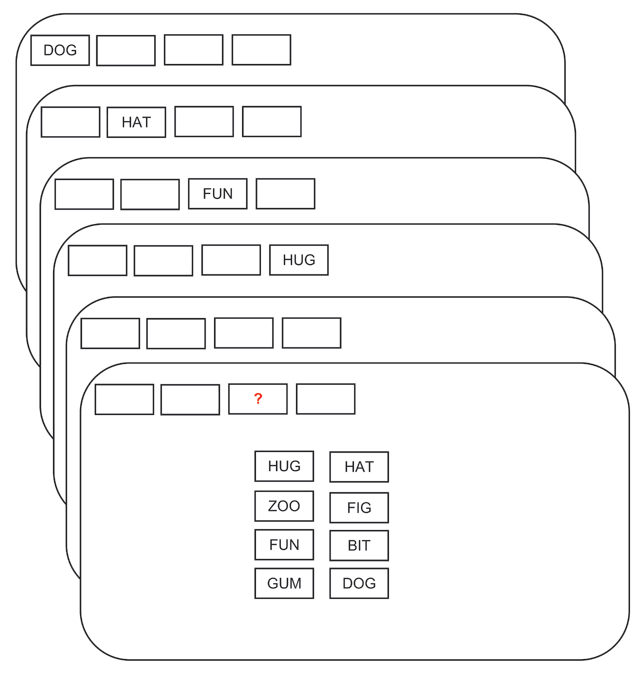
Ein Beipieltrial. Den Versuchspersonen wurden Wörter der einstudierten Liste gezeigt. Die Position des Testwortes wurde am Schluss gezeigt, und die das Wort musste wiedergegeben werden.

Figure 1: Ein Beipieltrial. Den Versuchspersonen wurden Wörter der einstudierten Liste gezeigt. Die Position des Testwortes wurde am Schluss gezeigt, und die das Wort musste wiedergegeben werden.

Wir schauen uns hier der Einfachheit halber nur die Daten einer Person an.

Daten vorbereiten

Wir laden zuerst die Daten, und zentrieren den Prädiktor set_size, um die Interpretation der Koeffizienten einfacher zu machen.

Wenn wir den Prädiktor zentrieren, können wir den Intercept interpretieren - das ist dann der Wert des linearen Prädiktors am Mittelwert von set_size.

library(tidyverse)

df_recall <- read_csv("https://raw.githubusercontent.com/kogpsy/neuroscicomplab/main/data/df_recall.csv")

df_recall <- df_recall %>%
  mutate(c_set_size = set_size - mean(set_size))

df_recall

# A tibble: 92 x 8
    subj set_size correct trial session block tested c_set_size
   <dbl>    <dbl>   <dbl> <dbl>   <dbl> <dbl>  <dbl>      <dbl>
 1    10        4       1     1       1     1      2         -1
 2    10        8       0     4       1     1      8          3
 3    10        2       1     9       1     1      2         -3
 4    10        6       1    23       1     1      2          1
 5    10        4       1     5       1     2      3         -1
 6    10        8       0     7       1     2      5          3
 7    10        6       1    10       1     2      3          1
 8    10        2       1    19       1     2      1         -3
 9    10        2       1     9       1     3      2         -3
10    10        6       0    16       1     3      5          1
# … with 82 more rows

Wir haben für jede set_size 23 Trials.

df_recall %>%
    group_by(set_size) %>%
    count()

# A tibble: 4 x 2
# Groups:   set_size [4]
  set_size     n
     <dbl> <int>
1        2    23
2        4    23
3        6    23
4        8    23

Wir interessieren uns für die Variablen c_set_size und correct, welche angibt, ob die Antwort richtig oder falsch war. Insbesondere interessieren wir uns dafür, ob es einen linearen Zusammenhang zwischen c_set_size und correct gibt. Wir verwenden dafür die Formel correct ~ 1 + c_set_size.

Bevor Sie mit der Bayesianischen Analyse beginnen, versuchen Sie die Accuracy dieser Person für jede Wortlistenlänge zu bestimmen.

df_recall %>% 
  group_by(set_size) %>% 
  summarise(accuracy = mean(correct),
            sd = sd(correct))

# A tibble: 4 x 3
  set_size accuracy    sd
     <dbl>    <dbl> <dbl>
1        2    1     0    
2        4    0.957 0.209
3        6    0.913 0.288
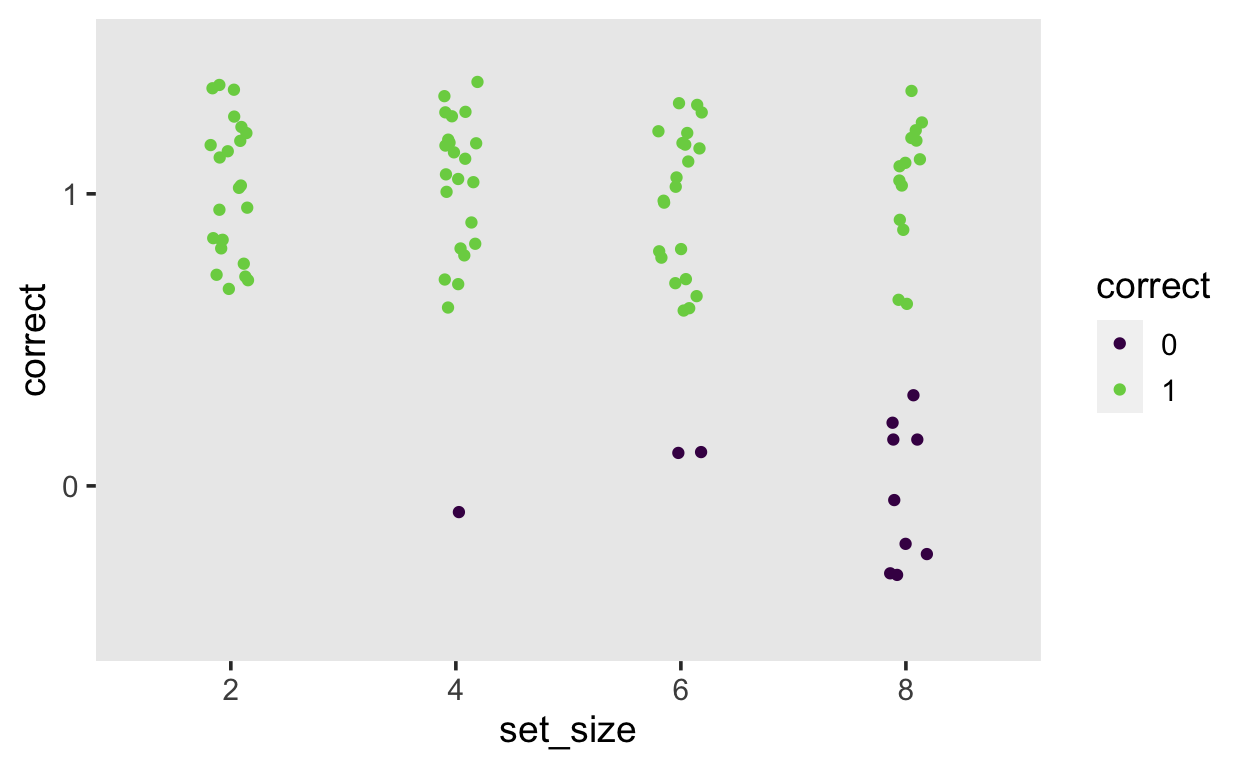
4        8    0.609 0.499

df_recall%>% 
  mutate(across(c(set_size, correct), ~as_factor(.))) %>% 
  ggplot(aes(set_size, correct, color = correct)) +
  geom_jitter(width = 0.1) +
  scale_color_viridis_d(end = 0.8)

Likelihood

Wir schreiben nun die Verteilung der Daten auf.

\[ correct_i \sim Bernoulli(\theta_{i})\]

Jede Antwort \(i\) kommt also aus einer Bernoulliverteilung, und ist mit Wahrscheinlichkeit \(\theta_i\) richtig, und mit Wahrscheinlichkeit \(1-\theta_i\) falsch. Diese Wahrscheinlichkeit soll anhand eines linearen Prädiktors vohergesagt werden.

\[ g(\theta_i) = logit(\theta_i) = b_0 + b_{set\_size} \cdot set\_size_i \]

Die logit Funktion ist

\[ logit(\theta) = log \bigg( \frac{\theta}{(1-\theta)} \bigg) \] und wird auch auch log-odds genannt, da sie den Logarithmus der odds (Wettquotienten) wiedergibt. Es folgt also

\[ log \bigg( \frac{\theta_i}{1-\theta_i} \bigg) = b_0 + b_{set\_size} \cdot set\_size_i \] Dies bedeutet, dass die Koeffizienten \(b_0\) und \(b_{set\_size}\) einen additiven Effekt auf die log-odds haben. Wenn wenn den Effekt auf der Wahrscheinlichkeitsskala haben möchten, müssen wir die inverse Link Funktion anwenden, d.h. die logistische Funktion. Diese ist die kumulative logistische Verteilungsfunktion, plogis().

Wenn die log-odds z.B. 0.1 sind, dann ist die Wahrscheinlichkeit 0.52:

logodds <- 0.1
prob <- plogis(logodds)
prob

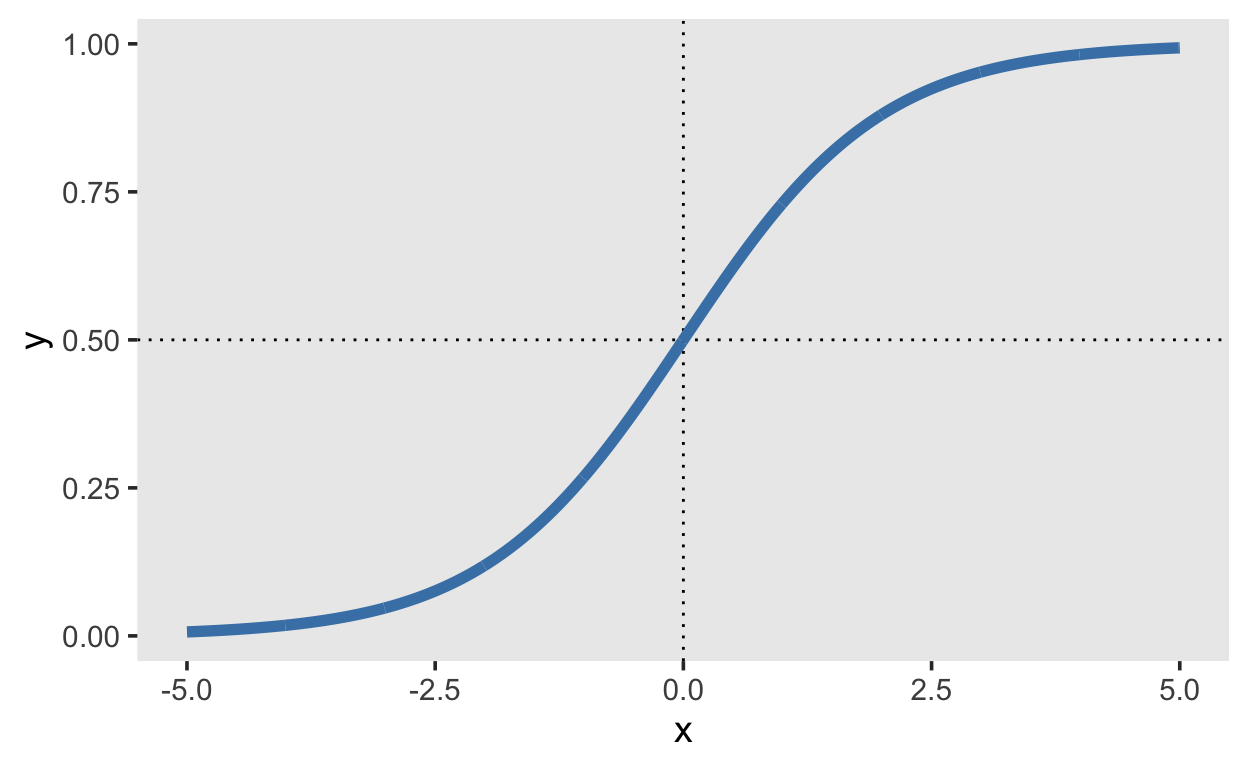
[1] 0.5249792

Versuchen Sie mit R herauszufinden, wie sich die Wahrscheinlichkeiten in als Funktion der log-odds verhalten (eine ähnliche Grafik wie in den Slides hilft).

d1 <- tibble(x = seq(-5, 5, by = 0.01),
            y = plogis(x))

d1 %>% 
    ggplot(aes(x, y)) +
    geom_hline(yintercept = 0.5, linetype = 3) +
    geom_vline(xintercept = 0, linetype = 3) +
    geom_line(size = 2, color = "steelblue")

Wenn wir uns mit log-odds auskennen, hilft uns dies, den Output einer logistischen Regression zu verstehen, und geeignete Priorverteilungen zu verwenden.

Priorverteilungen

Da wir den Prädiktor set_size zentriert haben, wird der Intercept \(b_0\) die log-odds einer korrekten Antwort für die mittlere Wortlistenlänge repräsentieren. Unser Prior sollte abhängig sein von der Schwierigkeit des Tasks. Wenn wir uns hier unsicher sind, können wir annehmen, dass die Person bei der mittleren Wortlistenlänge mit ungefähr gleicher Wahrscheinlichkeit \(\theta\) eine korrekte oder falsche Antwort gibt. Wenn \(\theta = 0.5\), dann sind die log-odds 0.

Wir können unsere Unsicherheit durch eine Normalverteilung mit einer Standardabweichung von ca. 1.0 ausdrücken. Dies bedeutet, dass ca. 95% der Verteilung im Bereich \([-2, 2]\)

Versuchen Sie dies mit der Funktion qlogis() zu demonstrieren.

qnorm(c(.025, .975), mean = 0, sd = 1.0)

[1] -1.959964  1.959964

Den Prior können wir so grafisch darstellen.

library(patchwork)

samples <- tibble(Intercept = rnorm(1e5, 0, 1.0),
                  p = plogis(Intercept))

p_logodds <- samples %>% 
  ggplot(aes(Intercept)) +
  geom_density() +
  ggtitle("Log-odds")

p_prob <- samples %>% 
  ggplot(aes(p)) +
  geom_density() +
  ggtitle("Probability")


p_logodds + p_prob

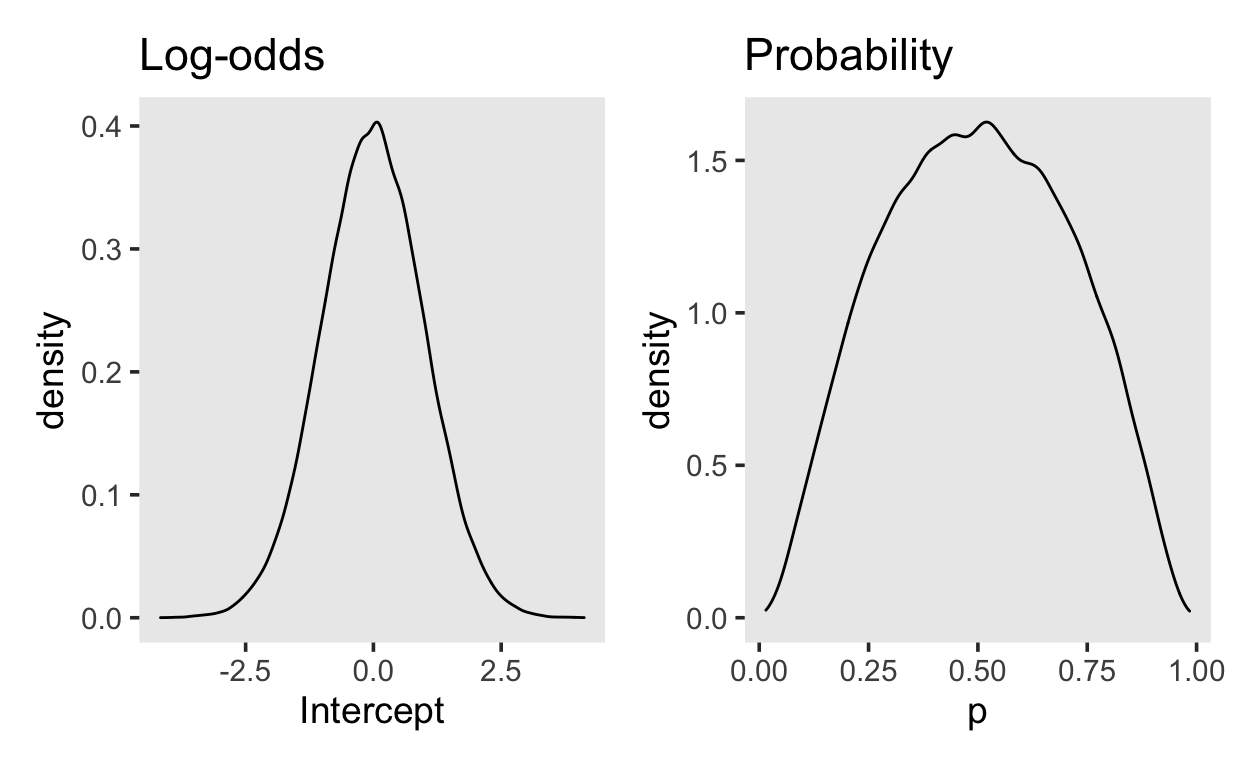
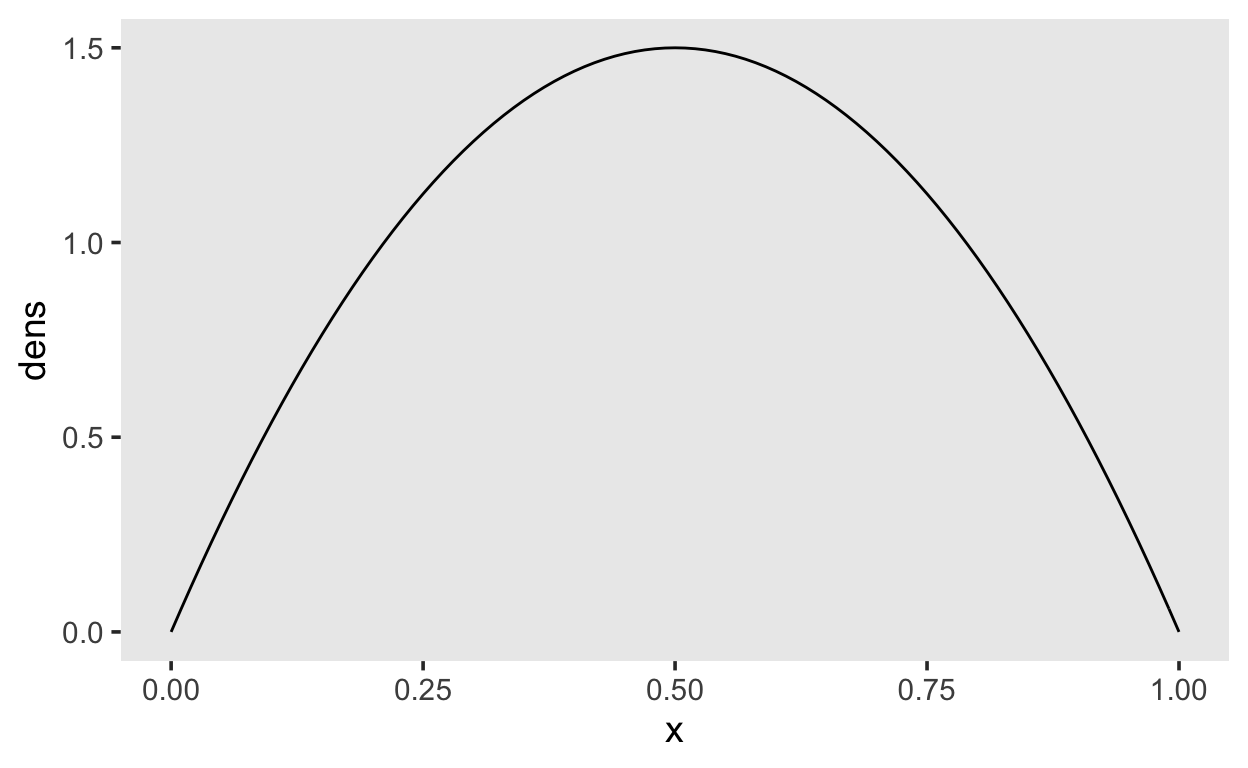
Unser normal(0, 1.0) Prior führt also zu einem Prior auf der Wahrscheinlichkeitsskala, welcher ungefähr einem beta(2, 2) Prior entspricht.

tibble(x = seq(0, 1, by = 0.01),
       dens =  dbeta(x, shape1 = 2, shape2 = 2)) %>% 
  ggplot(aes(x, dens)) +
  geom_line()

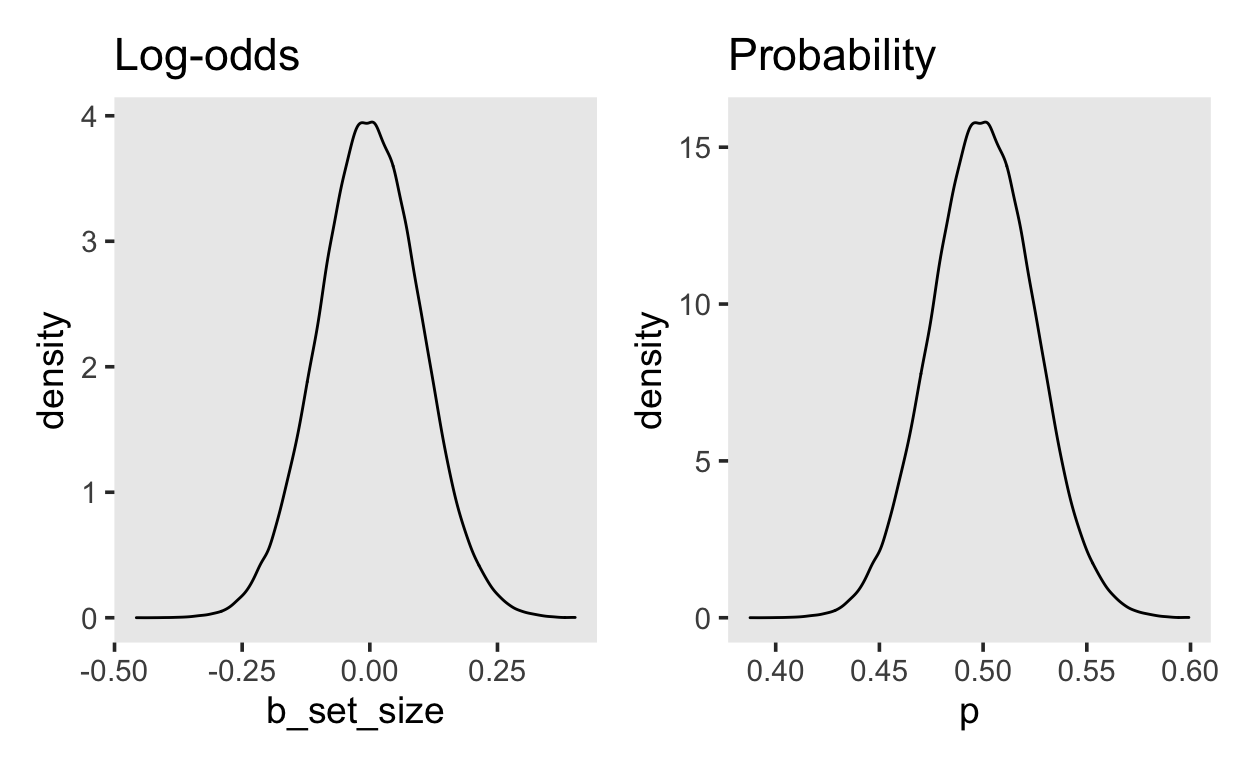
Für die set_size gehen wir davon aus, dass der Effekt auf die Wahrscheinlichkeit einer korrekten Antwort so ist, dass der Unterschied zwischen der kleinsten und grössten set_size ca. 0.4 ist. Das heisst, dass eine Erhöhung um eine Einheit zu einer Änderung der Wahrscheinlichkeit von ca. \(0.4/4 = 0.1\) führen sollte. Wir versuchen es mit einem normal(0, 0.1) Prior. Wir erwarten also einen Effekt im Bereich \([-0.2, 0.2]\) mit einer Wahrscheinlichkeit von 95%.

samples2 <- tibble(b_set_size = rnorm(1e5, 0, 0.1),
                          p = plogis(b_set_size))

p_logodds <- samples2 %>% 
  ggplot(aes(b_set_size)) +
  geom_density() +
  ggtitle("Log-odds")

p_prob <- samples2 %>% 
  ggplot(aes(p)) +
  geom_density() +
  ggtitle("Probability")


p_logodds + p_prob

Modell

Versuchen Sie, das Modell in brms zu schätzen.

Wir spezifizieren Verteilung der abhängigen Variable mit dem Argument family. Die Verteilung, hier bernoulli() nimmt selber ein Argument, welches die Link Funktion definiert.

Es gibt hier auch anderen Möglichkeiten als logit. Es kommen viele Verteilungsfunktionen in Frage—eine häufig benutzte Variante ist probit. Dies benutzt die kumulative Normalverteilung als Link Funktion.

library(brms)

priors <- prior(normal(0, 1.0), class = Intercept) +
    prior(normal(0, .1), class = b, coef = c_set_size)

m_recall <- brm(correct ~ 1 + c_set_size,
                family = bernoulli(link = logit),
                prior = priors,
                data = df_recall,
                file = "models/06-m_recall",
                file_refit = "on_change")

plot(m_recall)

Output

Versuchen Sie, die Koeffizienten zu interpretieren. Was ist der Intercept? Was ist der Effekt c_set_size?

summary(m_recall)

 Family: bernoulli 
  Links: mu = logit 
Formula: correct ~ 1 + c_set_size 
   Data: df_recall (Number of observations: 92) 
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup samples = 4000

Population-Level Effects: 
           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS
Intercept      1.82      0.29     1.29     2.44 1.00     2885
c_set_size    -0.18      0.08    -0.33    -0.03 1.00     3163
           Tail_ESS
Intercept      2407
c_set_size     2573

Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

m_recall %>% 
  mcmc_plot("b")

Interpretation:

Die Koeffizienten sind auf der log-odds Skala.

Der Intercept repräsentiert die log-odds einer korrekten Antwort bei einer mittleren Set Size.
Der Parameter c_set_size repräsentiert den Effekt der Set Size. Bei einer Erhähung um eine Einheit sinken die log-odds um ca. -0.18.

Wenn wir diese Effekte auf der Wahrscheinlichkeitsskala haben wollen, müssen wir die Posterior Samples extrahieren und anschliessend diese Samples mit der Umkehrfunktion der Linkfunktion transformieren. Diese Umkehrfunktion ist die logistische Funktion (plogis() in R).

samples1 <- tibble(posterior_samples(m_recall)) %>% 
  select(starts_with("b"))

Die Samples können wir nun zusammenfassen, z.B. mit den Funktionen aus dem tidybayes Package. Dafür macht es Sinn, die Samples auch mit einer Funktion die extrahieren, welche einen Dataframe im long-Format liefert.

library(tidybayes)

samples2 <- m_recall %>% 
  gather_draws(b_Intercept, b_c_set_size)

samples2 %>% 
  median_qi(.width = c(.95, .8, .5))

# A tibble: 6 x 7
  .variable    .value .lower  .upper .width .point .interval
  <chr>         <dbl>  <dbl>   <dbl>  <dbl> <chr>  <chr>    
1 b_c_set_size -0.179 -0.331 -0.0288   0.95 median qi       
2 b_Intercept   1.81   1.29   2.44     0.95 median qi       
3 b_c_set_size -0.179 -0.281 -0.0850   0.8  median qi       
4 b_Intercept   1.81   1.47   2.20     0.8  median qi       
5 b_c_set_size -0.179 -0.235 -0.130    0.5  median qi       
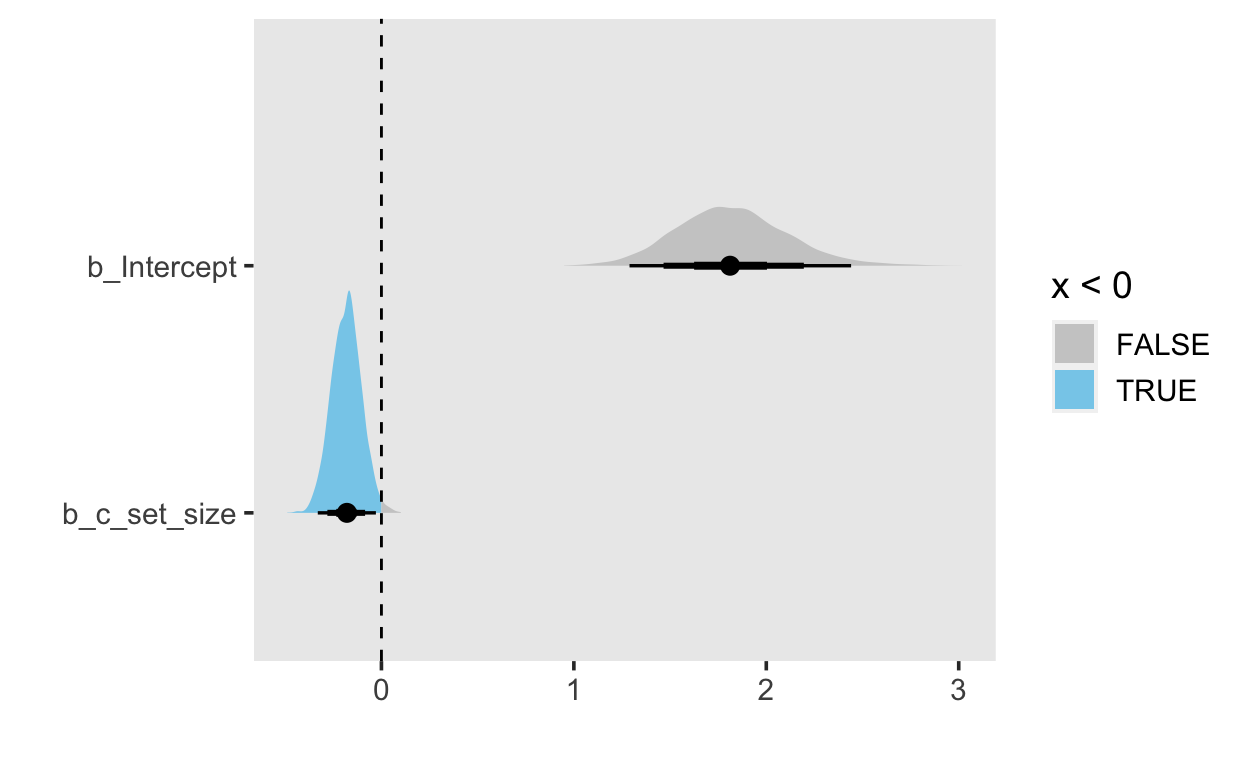
6 b_Intercept   1.81   1.62   2.00     0.5  median qi

samples2 %>% 
  ggplot(aes(.value, .variable, fill = stat(x < 0))) +
  stat_halfeye(.width = c(.95, .8, .5)) +
  geom_vline(xintercept = 0.0, linetype = "dashed") +
  scale_fill_manual(values = c("gray80", "skyblue")) +
  xlab("") + ylab("")

Effekte auf der Odds/Wahrscheinlichkeitsskala

samples_set_size <- m_recall %>% 
  gather_draws(b_c_set_size) %>% 
  ungroup() %>% 
  select(logodds = .value)

samples_set_size

# A tibble: 4,000 x 1
   logodds
     <dbl>
 1  -0.285
 2  -0.253
 3  -0.135
 4  -0.196
 5  -0.106
 6  -0.263
 7  -0.154
 8  -0.166
 9  -0.102
10  -0.245
# … with 3,990 more rows

samples_set_size <- samples_set_size %>% 
  mutate(odds = exp(logodds),
         prob = plogis(logodds))

samples_set_size

# A tibble: 4,000 x 3
   logodds  odds  prob
     <dbl> <dbl> <dbl>
 1  -0.285 0.752 0.429
 2  -0.253 0.776 0.437
 3  -0.135 0.874 0.466
 4  -0.196 0.822 0.451
 5  -0.106 0.899 0.474
 6  -0.263 0.769 0.435
 7  -0.154 0.857 0.462
 8  -0.166 0.847 0.459
 9  -0.102 0.903 0.474
10  -0.245 0.783 0.439
# … with 3,990 more rows

samples_set_size %>% 
  pivot_longer(everything(), 
               names_to = "Parameter", 
               values_to = "value") %>% 
  group_by(Parameter) %>% 
  median_qi()

# A tibble: 3 x 7
  Parameter  value .lower  .upper .width .point .interval
  <chr>      <dbl>  <dbl>   <dbl>  <dbl> <chr>  <chr>    
1 logodds   -0.179 -0.331 -0.0288   0.95 median qi       
2 odds       0.836  0.718  0.972    0.95 median qi       
3 prob       0.455  0.418  0.493    0.95 median qi

Da der Effekt ist auf der logodds Skala additiv, auf der odds Skala multiplikativ, und auf der prob Skala non-linear.

conditional_effects(m_recall)

Wenn wir die erwarteten bedingten Wahrscheinlichkeiten wollen, ist es einfacher, die predict() Funktion zu benutzen.

predict(m_recall, newdata = tibble(c_set_size = c(-1, 0, 1)))

     Estimate Est.Error Q2.5 Q97.5
[1,]  0.87675 0.3287651    0     1
[2,]  0.85650 0.3506258    0     1
[3,]  0.82950 0.3761185    0     1

Bayes Factor

Bayes Factors schätzen funktioniert genauso wie bei den bisherigen Modellen. Wir schätzen das Modell nochmals, mit dem Argument sample_prior = TRUE, und können dann die hypothesis() Funktion benutzen, um das Savage-Dickey Densoty Ratio zu bestimmen, (oder die bayes_factor() Funktion aus dem bridgesampling Package, wenn wir save_pars = save_pars(all = TRUE) benutzen.

priors <- prior(normal(0, 1.0), class = Intercept) +
    prior(normal(0, .1), class = b, coef = c_set_size)

m_recall_2 <- brm(correct ~ 1 + c_set_size,
                family = bernoulli(link = logit),
                prior = priors,
                data = df_recall,
                sample_prior = TRUE,
                file = "models/06-m_recall_2",
                file_refit = "on_change")

Mit hypothesis() erhalten wir folgenden Bayes Factor für die Nullhypothese.

BF01 <- hypothesis(m_recall_2, "c_set_size = 0")

Der Bayes Factor für die Alternativhypothese ist:

BF10 <- 1/BF01$hypothesis$Evid.Ratio

BF10

[1] 8.200683

Oberauer, Klaus. 2019. “Working Memory Capacity Limits Memory for Bindings.” Journal of Cognition 2 (1, 1): 40. https://doi.org/10.5334/joc.86.

Datenanalyse

Logistische Regression

Daten vorbereiten

Likelihood

Priorverteilungen

Modell

Output

Effekte auf der Odds/Wahrscheinlichkeitsskala

Bayes Factor

References

Corrections

Reuse

Citation