RStudio Projekte
Ich empfehle (wie schon in den Statistik Übungen) immer in einem RStudio Projekt zu arbeiten. Als Faustregel: jedes Datenanalyseprojekt kriegt ein eigenes RStudio Projekt. Die Vorteile sind:
- Man kann das Projekt schliessen und wieder im gleichen Zustand öffnen, d.h. alle offenen Files werden wieder hergestellt. So kann man z.B. eine Woche lang nicht an einem Projekt arbeiten, und danach wieder in dem Zustand weiterfahren, in dem man aufgehört hat.
- Man muss keine absoluten Pfade benutzen, sondern nur relative.
Rmarkdown
Rmarkdown ist eine Erweiterung der Markdown Sprache, welche wiederum eine einfache Sprache ist, um Text zu formattieren.
Mit Markdown ist es möglich, HTML oder LaTeX zu erstellen, ohne das man selber viel HTML/LaTeX kennen muss. LaTeX ist vor allem dann gut, wenn man viele Formeln benutzt, oder komplizierte Dokumente erstellt.
Rmarkdown erlaubt zusätzlich die Einbindung von R Code; dieser wird zuerst evaluiert, und der Ouput wird zu Markdown konvertiert. Damit lassen sich Paper und Bachelor/Masterarbeiten schreiben, was sehr sinnvoll ist, wenn man mit R arbeitet.
Ein weiterer Grund, Rmarkdown zu benutzen, ist Reproduzierbarkeit. Man kann Code für Datenanalyse direkt in ein Manuskript einbinden, so dass die Resultate immer up-to-date sind, und nicht zwischen Dokumenten hin-und her kopiert werden müssen (was sehr fehleranfällig ist).
Ein exzellente Einführung in Rmarkdown finden Sie im Blog von Danielle Navarro: Einführung in Rmarkdown.
Schauen Sie sich die Slides an.
RStudio macht es sehr einfach, mit Rmarkdown zu arbeiten. Un ein neues Dokument zu erstellen, öffnen Sie das File Menu. Dort wählen Sie New File aus, und dann Rmarkdown....
Sie sehen dann dieses Dialogfenster:
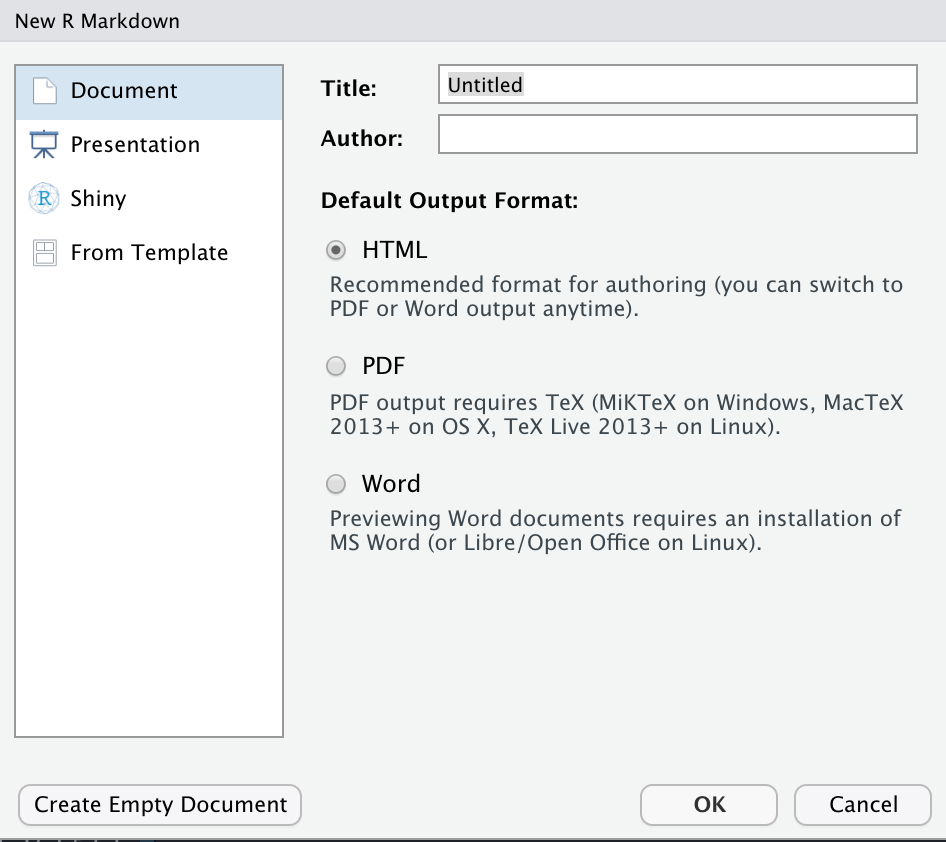
Hier können Sie das Output Format bestimmen: HTML, PDF (LaTeX), oder Word.
Nachdem Sie OK geklickt haben, erhalten Sie ein Rmarkdown Template. Dies können Sie mit der Knit Funktion zu einem HTML (oder PDF, Word) konvertieren. Zuerst müssen Sie das Dokument jedoch speichern.
Erstellen Sie ein Rmarkdown Dokument und speichern Sie es. Probieren Sie verschiedene Output Formate, und knitten Sie das Dokument.
In der nächsten Übung machen wir zwei ganz wichtige Dinge: wir benutzen Rmarkdown, und wir generieren Daten. Genauer gesagt benutzen wir ein statistisches (probabilistisches) Modell, um Zufallszahlen zu generieren. In dieser Übung generieren wir Daten, die dem statistischen Modell eines t-Tests entsprechen.
Fügen Sie folgenden R Code in einen oder (noch besser) mehreren Code Chunks ein. Benützen Sie Markdown Text, um das Ganze zu kommentieren., d.h. die Kommentare zwischen den R Code Zeilen könnten auch als Prosa zwischen R Code Chunks stehen.
library(tidyverse)
set.seed(12)
# Number of people wearing fancy hats
N_fancyhats <- 50
# Number of people not wearing fancy hats
N_nofancyhats <- 50
# Population mean of creativity for people wearing fancy hats
mu_fancyhats <- 103
# Population mean of creativity for people wearing no fancy hats
mu_nofancyhats <- 98
# Average population standard deviation of both groups
sigma <- 15
# Generate data
fancyhats = tibble(Creativity = rnorm(N_fancyhats, mu_fancyhats, sigma),
Group = "Fancy Hat")
nofancyhats = tibble(Creativity = rnorm(N_nofancyhats, mu_nofancyhats, sigma),
Group = "No Fancy Hat")
FancyHat <- bind_rows(fancyhats, nofancyhats) %>%
mutate(Group = fct_relevel(as.factor(Group), "No Fancy Hat"))
# plot both groups
FancyHat %>%
ggplot() +
geom_boxplot ((aes(y = Creativity, x = Group))) +
labs(title= "Box Plot of Creativity Values") +
theme_bw()
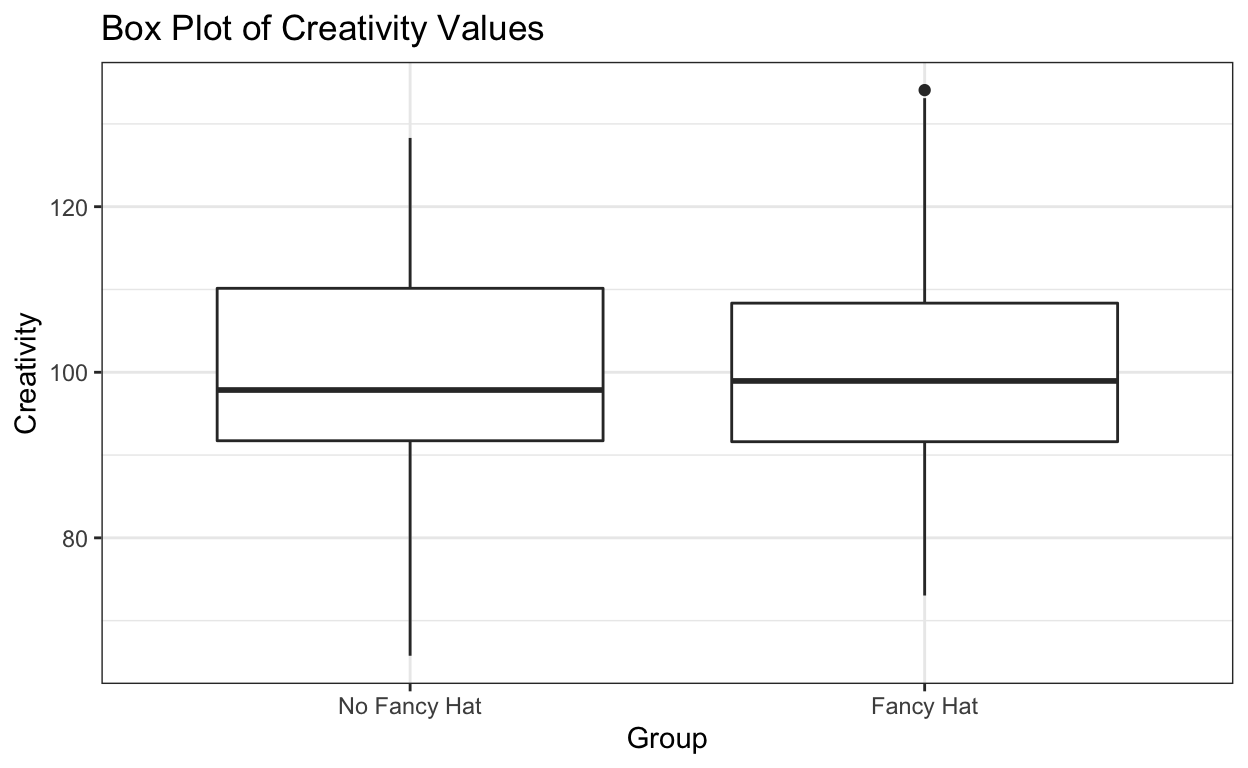
Mit diesem Code simulieren Sie zwei experimentelle Gruppen, mit je 50 Teilnehmern. Die eine Gruppe trug “fancy hats”, die andere Gruppe nicht. Wir generieren normalverteilte Zufallszahlen—für die Fancy Hat Gruppe mit \(\mu=103\), für die No Fancy Hat mit \(\mu=98\). Mit bind_rows() fügen wir beide Dataframes zusammen, und am Schluss machen wir einen Boxplot.
Wenn Sie eine R Code Chunk einfügen, z.B. mit Code > Insert Chunk, erhalten Sie ein Options Icon am oberen rechten Rand des Chunks. Hier können Sie wählen, ob der Code/Output angezeigt wird.
Führen Sie einen (gerichteten) t-Test in einem Code Chunk durch. Zur Erinnerung: Sie brauchen die Funktion t.test() mit den Argumenten alternative = "less" und var.equal = TRUE.
Lösung
Two Sample t-test
data: Creativity by Group
t = -0.63685, df = 98, p-value = 0.2629
alternative hypothesis: true difference in means between group No Fancy Hat and group Fancy Hat is less than 0
95 percent confidence interval:
-Inf 2.647764
sample estimates:
mean in group No Fancy Hat mean in group Fancy Hat
99.20888 100.85606 Übung
Das gleiche Modell können Sie (für den ungerichteten Fall) auch als Allgemeines Lineares Modell formulieren.
Lösung
Call:
lm(formula = Creativity ~ Group, data = FancyHat)
Residuals:
Min 1Q Median 3Q Max
-33.448 -8.578 -1.704 8.645 33.224
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 99.209 1.829 54.245 <2e-16 ***
GroupFancy Hat 1.647 2.586 0.637 0.526
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 12.93 on 98 degrees of freedom
Multiple R-squared: 0.004121, Adjusted R-squared: -0.006041
F-statistic: 0.4056 on 1 and 98 DF, p-value: 0.5257Lösung
# A tibble: 1 x 3
`No Fancy Hat` `Fancy Hat` diff
<dbl> <dbl> <dbl>
1 99.2 101. -1.65