neuroscicomplab: Übung 5

Andrew Ellis

Die Aufgaben, die Sie bearbeiten sollen, finden Sie in einem gelben Kasten. Optionale Aufgaben sind in orangen Kästen.

Sie haben für diese Übung 8 Tage Zeit. Laden Sie bitte diesmal Ihre Lösung als ZIP File bis Donnerstag, 13. Mai um 00:00 Uhr, in den Order für Übung 5 auf ILIAS. Das ZIP File sollte sowohl das Rmarkdown File als auch das generierte HTML File enthalten.

Nennen Sie Ihr File Matrikelnummer_Nachname_uebung-5.zip.

Bei dieser Übung werden keine Lösungen akzeptiert, bei denen nichts geschrieben wurde. Dies bedeutet: wenn in der Aufgabe steht “Bitte schreiben Sie kurz…” dann erwarte ich auch, dass etwas geschrieben wird.

Aufgabenstellung

Wir untersuchen in dieser Aufgabe den Zusammenhang zwischen Attentional Load und Pupillengrösse. Wir verwenden dafür die Daten aus der Studie von Wahn et al. (2016). Es ist bekannt, dass die Grösse unserer Pupillen mit dem einfallenden Licht zusammenhängt. Es wird jedoch auch seit längerem vermutet, dass die Pupillengrösse mit kognitiven Prozessen zusammenhängt.

In dieser Studie untersuchten Wahn et al. (2016) den Einfluss des “attentional load” auf die Pupillengrösse von 20 Versuchspersonen anhand eines “Multiple Object Tracking” (MOT) Tasks.

Ein Beispieltrial ist in Grafik 1 dargestellt.

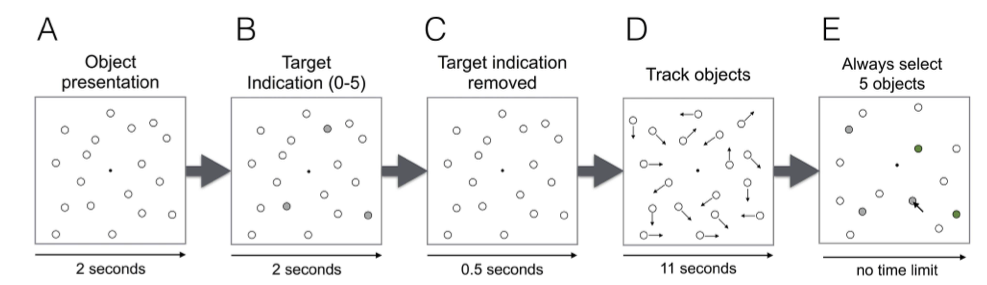
Beispieltrial eines Multiple Object Tracking Tasks. Versuchspersonen sahen zuerst 18 Objekte auf einem Bildschirm (A). Danach wurden zwischen 0 und 5 dieser Objekte anhand einer Markierung ausgewählt (B)---diese Objekte mussten visuell verfolgt werden. Die Markierungen verschwand wieder (C), und die Objekte fingen an, sich während 11 Sekunden zu bewegen (D). Am Ende des Trials mussten die Versuchspersonen angeben, welche Objekte sie verfolgt hatten. Die Anzahl der zu verfolgenden Objekte gilt als Mass für attentional load.

Figure 1: Beispieltrial eines Multiple Object Tracking Tasks. Versuchspersonen sahen zuerst 18 Objekte auf einem Bildschirm (A). Danach wurden zwischen 0 und 5 dieser Objekte anhand einer Markierung ausgewählt (B)—diese Objekte mussten visuell verfolgt werden. Die Markierungen verschwand wieder (C), und die Objekte fingen an, sich während 11 Sekunden zu bewegen (D). Am Ende des Trials mussten die Versuchspersonen angeben, welche Objekte sie verfolgt hatten. Die Anzahl der zu verfolgenden Objekte gilt als Mass für attentional load.

Üblicherweise wird in Pupillengrössen Exerimenten die Anteilsmässige Veränderung der Pupillengrössen in Prozent angegeben. Wir verwenden hier jedoch der Einfachheit halber die Rohwerte (gemittelt über beide Augen). Wir nehmen an, dass ein grösserer attentional load zu einer Erweiterung der Pupillen führt, und zwar nehmen wir hier an, dass der Zusammenhang zwischen attentional load und Pupillengrösse linear ist.

Daten laden

Wir laden zuerst die benötigten Packages, und die Daten. Die Personenvariable wird zu einem Faktor konvertiert. Ausserdem erstellen wir einen Faktor attentional_load, damit wir die Daten einfacher grafisch darstellen können.

library(tidyverse)
library(brms)

# mehrere Cores parallel für sampling
options(mc.cores = parallel::detectCores())
# ggplot Optionen
theme_set(theme_grey(base_size = 14) +
            theme(panel.grid = element_blank()))

pupilsize <- read_csv("https://raw.githubusercontent.com/kogpsy/neuroscicomplab/main/data/df_pupil_complete.csv") %>% 
  mutate(subj = as_factor(subj),
         attentional_load = as_factor(load))

glimpse(pupilsize)

Rows: 2,228
Columns: 5
$ subj             <fct> 701, 701, 701, 701, 701, 701, 701, 701, 701…
$ trial            <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, …
$ load             <dbl> 2, 1, 5, 4, 0, 3, 0, 4, 2, 3, 5, 1, 4, 3, 0…
$ p_size           <dbl> 1021.4086, 951.4349, 1063.9569, 913.4871, 6…
$ attentional_load <fct> 2, 1, 5, 4, 0, 3, 0, 4, 2, 3, 5, 1, 4, 3, 0…

Die Variable p_size ist die Pupillengrösse, load ist der attentional load als numerische Variable, attentional_load ist der Faktor. subj ist die Versuchspersonennummer, und trial die Durchgangsnummer.

Wir haben pro Person eine unterschiedliche Anzahl Trials. Bei Vpn 701 handelt es sich wohl um Daten aus einer Pilotstudie.

pupilsize %>% 
  group_by(subj) %>% 
  count()

# A tibble: 20 x 2
# Groups:   subj [20]
   subj      n
   <fct> <int>
 1 701      41
 2 702     119
 3 703     120
 4 704     111
 5 705      99
 6 706     120
 7 707     120
 8 708     119
 9 709     119
10 710     117
11 711     120
12 712     120
13 713     120
14 714     120
15 715     120
16 716      65
17 717     120
18 718     120
19 719     118
20 720     120

Aufgaben

Aufgabe 1

Fassen Sie die Daten für jede Person pro attentional load Bedingung zusammen (Mittelwert, Standardfehler), und speichern Sie dies als Dataframe (benutzen Sie den attentional_load Faktor, d.h. group_by(subj, attentional_load)).
Stellen Sie Mittelwert plus Fehlerbalken für jede Person in jeder Bedingung dar. Dies ist einfacher, als es sich anhört (benutzen Sie facet_wrap(~subj, scales = "free_y")). Stellen Sie attentional_load auf der X-Achse dar, die mittlere Pupillengrösse auf der Y-Achse.
Beschreiben Sie in Worten (kurz) was sie hier sehen. Ist eine Tendenz ersichtlich? Ist diese bei jeder Person feststellbar? Gibt es Unterschiede zwischen den Personen?

Aufgabe 2

Sie sehen hier die mittlere Pupillengrösse pro attentional load Bedingung, aggregiert über Versuchspersonen. Die Fehlerbalken sind Standardfehler, welche die Messwiederholung berücksichtigen.

Beschreiben Sie in Worten (kurz) was sie hier sehen. Ist eine Tendenz ersichtlich?

agg <- Rmisc::summarySEwithin(by_subj,
                               measurevar = "mean",
                               withinvars = "attentional_load",
                               idvar = "subj",
                               na.rm = FALSE,
                               conf.interval = .95)

agg %>% 
  ggplot(aes(attentional_load, mean)) +
  geom_line(aes(group = 1), linetype = 3) +    
  geom_errorbar(aes(ymin = mean-se, ymax = mean+se),
                width = 0.2, size=1, color="blue") +
  geom_point(size = 4)

Wir benutzen nun den Prädiktor load, um die Pupillengrösse mit einem Bayesianischen Multilevel vorherzusagen. Wir nehmen an, dass die Pupillengrösse bedingt normalverteilt ist (Diese Annahme ist vertretbar; obwohl eine Grösse niemals negativ sein darf, sind hier weit genug weg von 0).

Da die Personen sich ähnlich sind, sich jedoch in ihrer Pupillengrösse aufgrund ihrer Anatomie unterscheiden, benutzen wir ein partial-pooling Modell.

Annahmen:

Die Outcome variable ist bedingt normalverteilt (oder die Fehler sind normalverteilt).
Es gibt einen linearen Zusammenhang zwischen attentional load und Pupillengrösse.
Die Personen stammen alle aus derselben Gruppe, aber unterschieden sich voneinander. Wir versuchen, den Mittelwert dieser Gruppe zu schätzen, und gleichzeitig, die Abweichung vom Mittelwert für jede Person.

Um die Interpretation eines Intercepts einfacher zu machen, zentrieren wir die Prädiktorvariable load, und speichern die zentrierte Variable als c_load. Der Intercept entspricht damit in unserem Regressionsmodell dem erwarteten Wert der abhängigen Variable bei einem mittleren attentional load (an der Stelle 0 von c_load).

pupilsize <- pupilsize %>%
   mutate(c_load = load - mean(load))

Aufgabe 3

Schreiben Sie die Formel für dieses Modell auf. Sie wollen die erwartete Pupillengrösse als lineare Funktion des attentional load vorhersagen, mit “varying effects” für den Achsenabschnitt und den Koeffizienten von c_load.
Untersuchen Sie mit get_prior() die Default Priors.

Wählen Sie für den Koeffizienten von c_load eine Normalverteilung mit Mittelwert 0 und einer Standardabweichung von 100. Dies bedeutet, dass wir mit 95% Sicherheit erwarten, dass der Effekt von c_load ungefähr im Bereich [-200, 200] liegt. Genauer können wir das so ausdrücken:

qnorm(c(.025, .975), mean = 0, sd = 100)

[1] -195.9964  195.9964

Aufgabe 4

Schätzen Sie das Modell mit Ihrer Formel und dem Prior für den Regressionskoeffizienten mit brms. Benutzen Sie das Argument control = list(max_treedepth = 12), damit Sie von Stan keine Warnungen erhalten.
Schauen Sie sich die summary() an. Ist alles in Ordnung?
Stellen Sie die Population-Level Effects grafisch dar (siehe Code weiter unten). Versuchen Sie, diese zu interpretieren.

Mit folgenden Code können Sie die Population-Level Effects darstellen. Der Output von brms wurde hier als m1 gespeichert.

library(patchwork)

p_intercept <- m1 %>% 
  mcmc_plot("b_Intercept", point_est = "mean", prob = 0.8, prob_outer = 0.95)

p_attentionalload <- m1 %>% 
  mcmc_plot("b_c_load", point_est = "mean", prob = 0.8, prob_outer = 0.95)

p_intercept / p_attentionalload

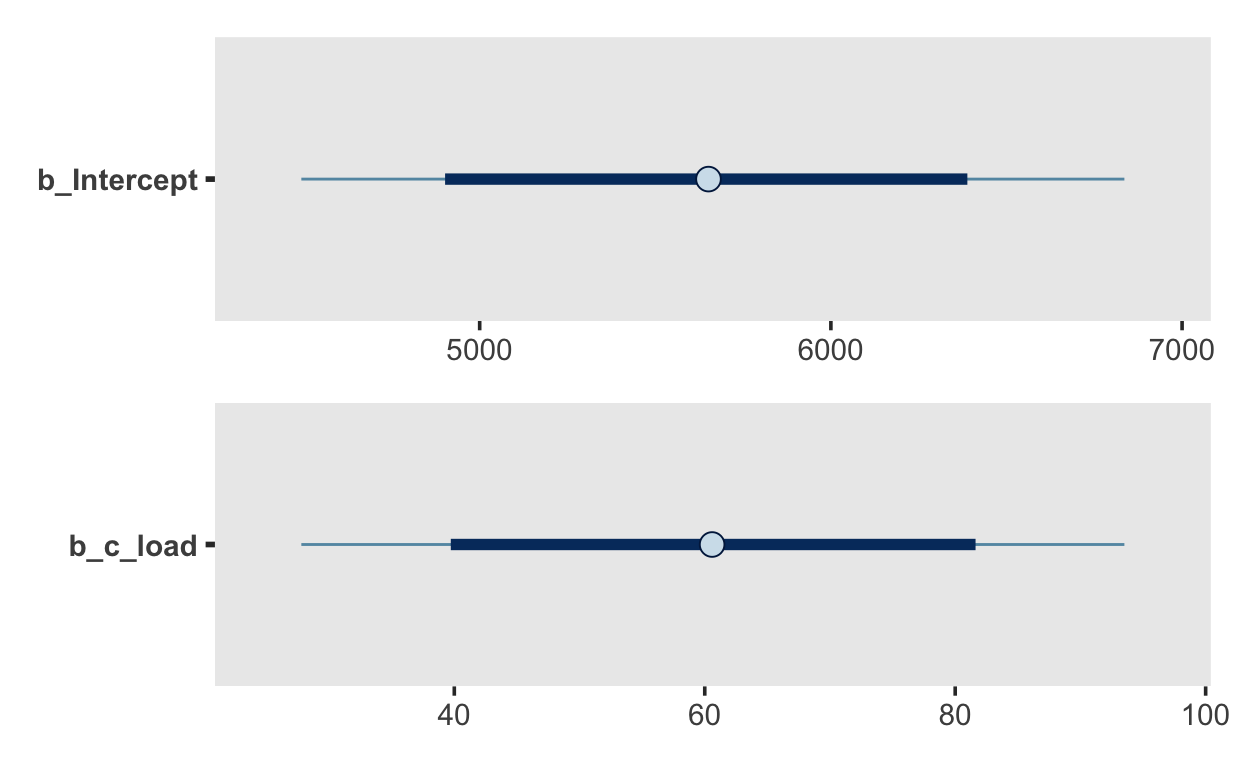
Mit der Funktion conditional_effects() können Sie den bedingten Efekt des Prädiktors auf die abhängige Varaiable darstellen, mit einem 95% Credible Interval.

conditional_effects(m1, prob = 0.95)

Aufgabe 5

Schätzen Sie mit der Savage-Dickey Methode einen Bayes Factor für die Hypothese, dass der Effekt von attentional load > 0 ist. Um diese Hypothese auszudrücken benutzen wir den Prior prior(normal(0, 100), class = b, lb = 0). Das Argument lb = 0 heisst hier, der Parameter hat einen lower bound (Untergrenze) von 0. Dies führt dazu, dass alle Werte $\leq 0$ unmöglich sind, da sie eine Wahrscheinlichkeitsdichte von 0 haben. Vergessen Sie nicht das Argument sample_prior = TRUE, damit die Samples aus den Prior Verteilungen gespeichert werden.
Berichten Sie den Bayes Factor (Wenn Sie den Ouput der hypothesis() Funktion als bf speichern, dann ist der BF 1/bf$hypothesis$Evid.Ratio).

m_savage_dickey <- brm(___ ~ ___,
          prior = prior(normal(0, 100), class = b, lb = 0),
          data = pupilsize,
          sample_prior = TRUE,
          control = list(max_treedepth = 12))

Optionale Aufgabe

Versuchen Sie, mit der Funktion bayes_factor() einen Bayes Factor für die Hypothese, dass der Effekt von attentional load > 0 ist. Sie brauchen dafür zwei Modelle; eines mit dem Population-Level Effekt von c_load, das andere ohne diesen Effekt (aber sonst in jeder Hinsicht identisch).

Sie brauchen die beiden zusätzlichen Argumente iter = 6e4 und save_pars = save_pars(all = TRUE). Mit dem ersteren erhalten Sie 60000 Samples aus dem Posterior, mit zweiterem speichern Sie die Log Likelihood.

Achtung: Wenn Sie das Modell selber schätzen wollen, müssen Sie damit rechnen, dass es sehr lange dauert.

m_positive <- brm(p_size ~ 1 + c_load + (1 + c_load | subj),
          prior = prior(normal(0, 100), class = b, lb = 0),
          data = pupilsize,
          iter = 6e4,
          save_pars = save_pars(all = TRUE),
          control = list(max_treedepth = 12),
          file = "models/ex5-m_positive",
          file_refit = "on_change")

m_null <- brm(p_size ~ 1 + (1 + c_load | subj),
          data = pupilsize,
          iter = 6e4,
          save_pars = save_pars(all = TRUE),
          control = list(max_treedepth = 12),
          file = "models/ex5-m_null",
          file_refit = "on_change")

BF <- bayes_factor(m_positive, m_null)

Mathot, Sebastiaan. 2018. “Pupillometry: Psychology, Physiology, and Function.” Journal of Cognition 1 (1, 1): 16. https://doi.org/10.5334/joc.18.

Wahn, Basil, Daniel P. Ferris, W. David Hairston, and Peter König. 2016. “Pupil Sizes Scale with Attentional Load and Task Experience in a Multiple Object Tracking Task.” PLOS ONE 11 (12): e0168087. https://doi.org/10.1371/journal.pone.0168087.

Übung 5

Aufgabenstellung

Daten laden

Aufgaben

References

Corrections

Reuse

Citation