flowchart TD i((Input)):::A --> p((Position)):::B classDef A fill:#ffffff, r:40px classDef B fill:#e5e4e4
Einführung
Uns interessiert, wie Daten entstanden sind. Wir können Daten deskriptiv beschreiben. Aber auch da haben wir bereits ein Vorstellung vom Prozess, der die Daten generiert hat. Das Ziel ist es, von den Daten zu lernen, sie zu beschreiben, vorherzusagen und zu erklären. Das folgende Beispiel basiert auf diesem Buch.
Planetare Bewegung
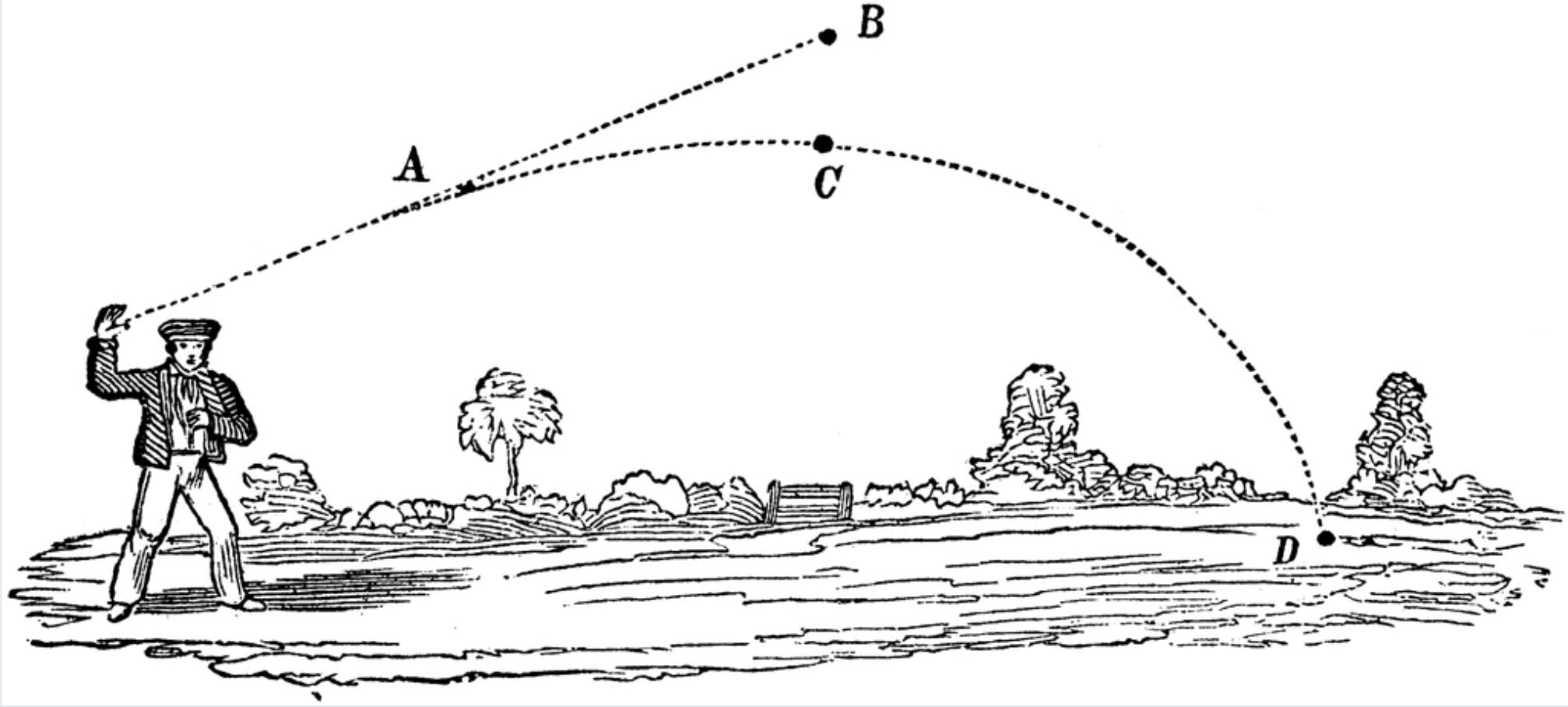
Beobachtung/Daten:
- Position der Planeten am Himmel über die Zeit
- Einige Planeten änderen plötzlich ihre Richtung
- Nach einiger Zeit nehmen sie ihren ursprünglichen Weg wieder auf

Geozentrisches Modell
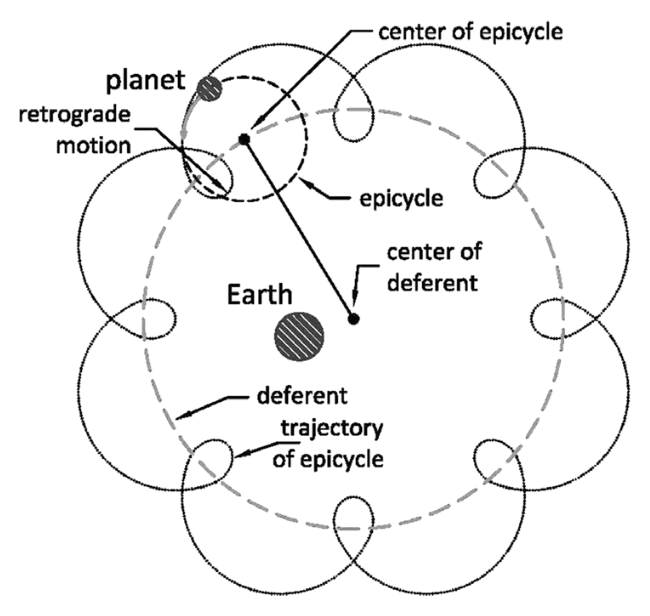
Heliozentrisches Modell

👉 Die Daten lassen sich nur mit einem Modell des zugrunde liegenden Prozesses erklären
👉 Modelle an sich können nicht beobachtet werden
👉 Es gibt fast immer mehrere Modelle, welche die Daten erklären können
Daten generierender Prozess
Im Beispiel oben versuchen wir anhand der Daten heraus zu finden, wie das Universum aufgebaut ist. Wir verwenden ein Modell um Informationen aus den Daten zu gewinnen. Wechseln wir nun zu einem etwas einfacheren Beispiel. Stellen Sie sich vor wir werfen einen Stein. Die Endposition des Steins hängt von den Kräften ab, die auf den Stein wirken.
Verbales Modell
Beginnen wir mit einem verbalen Modell von diesem Prozess. Die Endposition des Steins hängt von der Kraft und der Richtung (Input) des Wurfs ab. Faktoren wie z.B. der Luftwiderstand oder die Gravitationskraft berücksichtigen wir vorerst nicht in unserem Modell, da sie konstant sind.
Den Prozess, der durch das verbale DAG beschrieben wird, wiederholen wir 10 Mal. Der Input bleibt konstant. Bei jeder Durchführung notieren wir die Endposition des Steins.
Überlegen Sie sich, wie diese Daten aussehen.
Simulieren (generieren) Sie diese Daten in R.
Machen Sie eine sinnvolle Abbildung der simulierten Daten.
Statistisches Modell
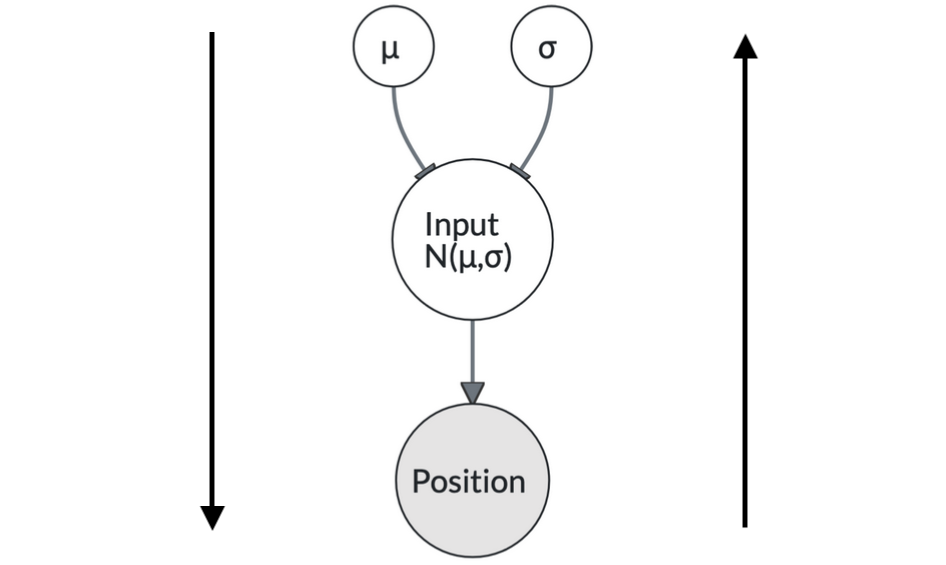
Berücksichtigen wir nun, dass der Stein von einer Person geworfen wird. Die Person zielt immer auf die gleiche Stelle (μ). Es ist aber unmöglich den Stein jedes Mal exakt gleich zu werfen. Es gibt also eine gewisse Variation der beobachteten Endpositionen (σ).
flowchart TD
mu((μ)):::a --> i((Input)):::A
s((σ)):::a --> i
i(("Input \n N(μ,σ)")):::A --> p((Position)):::B
classDef a fill:#ffffff, r:20px
classDef A fill:#ffffff, r:40px
classDef B fill:#e5e4e4
Den Prozess, der durch das (statistische) DAG beschrieben wird, wiederholen wir 10 Mal. Der Input ist nun normal verteilt. Bei jeder Durchführung notieren wir die Endposition des Steins.
Überlegen Sie sich, wie diese Daten aussehen.
Simulieren (generieren) Sie diese Daten in R.
Machen Sie eine sinnvolle Abbildung der simulierten Daten.
Simulation vs. Inferenz
mu = 5
sigma = 0.2
sim_data = tibble(
pos = rnorm(n = 10, mu, sigma)
)
head(sim_data)
head(d)
fit = lm(x ~ 1,
data = d)
coef(fit)["(Intercept)"]
sigma(fit)Simulation
Wir wählen Werte für die Modell-Parameter:
Damit können wir Daten simulieren:
# A tibble: 6 × 1
pos
<dbl>
1 5.24
2 4.84
3 5.23
4 5.07
5 5.16
6 5.00Inferenz (Parameterschätzung)
Wir beginnen mit Daten. Die Modell parameter sind uns nicht bekannt.
# A tibble: 6 × 1
x
<dbl>
1 4.31
2 4.26
3 4.23
4 4.44
5 4.38
6 4.12Basierend auf dem DAG formulieren wir ein lineares Modell. In diesem Fall schätzen wir nur den Intercept. Mit der Funktion lm() können wir die Parameter von diesem Modell schätzen (frequentistisch).
(Intercept)
4.29956 [1] 0.07045796Kategorialer Prädiktor - Planet
flowchart TD g((Gravitation)):::A --> p((Position)):::B i((Input)):::A --> p classDef A fill:#ffffff, r:40px classDef B fill:#e5e4e4
In diesem Fall haben wir die Endposition auf der Erde und auf dem Mond gemessen.
# A tibble: 6 × 2
planet pos
<chr> <dbl>
1 erde 5.19
2 erde 5.10
3 erde 5.14
4 mond 7.26
5 mond 6.87
6 mond 6.80Hier fügen wir dem linearen Modell einen kategorialen Prädiktor hinzu und schätzen die Parameter mit der Funktion lm().
lm(pos ~ 1 + planet,
data = d_cat)
Call:
lm(formula = pos ~ 1 + planet, data = d_cat)
Coefficients:
(Intercept) planetmond
5.000 2.058 Kontinuierlicher Prädiktor - Körpergrösse
flowchart TD g((Körpergrösse)):::A --> p((Position)):::B i((Input)):::A --> p classDef A fill:#ffffff, r:40px classDef B fill:#e5e4e4
Hier interessiert uns der Einfluss der Körpergrösse auf die Endposition eines geworfenen Steins.
# A tibble: 6 × 2
grösse pos
<dbl> <dbl>
1 165 5.06
2 165 5.11
3 165 5.08
4 170 6.04
5 170 6.19
6 170 5.87Hier fügen wir dem linearen Modell einen kontinuierlichen Prädiktor hinzu und schätzen die Parameter mit der Funktion lm().
lm(pos ~ 1 + grösse,
data = d_cont)
Call:
lm(formula = pos ~ 1 + grösse, data = d_cont)
Coefficients:
(Intercept) grösse
-30.1772 0.2122 Mit parameter recovery kann überprüft werden, wie gut die Parameter des Modells geschätzt werden können. Dazu werden zu erst Daten simuliert. In der anschliessenden Analyse der Daten sieht man wie nahe die geschätzten Parameter den wahren (in der Simulation verwendeten) sind.
Entscheiden Sie sich für ein Modell mit einem kategorialen oder einem kontinuierlichen Prädiktor.
Simulieren (generieren) Sie die entsprechenden Daten in R.
Analysieren Sie die Simulierten Daten mit dem entsprechenden Modell.
- Wie nahe ist die Schätzung an den wahren Parametern?
- Von welchen Faktoren könnte das abhängen?
Reuse
Citation
@online{fitze,
author = {Fitze, Daniel and Wyssen, Gerda},
title = {Einführung},
url = {https://kogpsy.github.io/neuroscicomplabFS24//pages/chapters/Modeling_1.html},
langid = {en}
}