Übung 4

Untersuchung eines präsymptomatischen Indikators für die Alzheimer-Krankheit

Authors

Affiliation

Andrew Ellis

Kognitive Psychologie, Wahrnehmung und Methodenlehre, Universität Bern

Gerda Wyssen

Kognitive Psychologie, Wahrnehmung und Methodenlehre, Universität Bern

Published

May 5, 2022

RStudio Projekt

👉 RStudio Projekt für diese Übung herunterladen

Sie finden darin ein Rmarkdown-File, welches Sie bearbeiten müssen, und den Datensatz.

Aufgaben

Die Übung 4 besteht aus den zwei folgenden Aufgaben:

1. Rmarkdown-File ausführen: In diesem File werden die Daten eingelesen, SDT Kennzahlen berechnet und Grafiken erstellt. Beantworten Sie die Fragen direkt im Rmarkdown-File. Das Rmarkdown-File muss von einer anderen Person ausgeführt werden können (Reproduzierbarkeit). Zeit: 1 Woche.

2. Peer Feedback: Mittels Ilias wird Ihnen das Rmarkdown-File einer anderen Person zugeordnet. Ihr Auftrag ist es, dieses Rmarkdown-File auszuführen und Feedback zu geben. Zeit: 1 Woche.

Einleitung

In Übung 4 arbeiten wir mit einem klinischen Datensatz. Das Ziel ist es, Sensitivität und Bias für zwei Gruppen von insgesamt 60 Patienten zu untersuchen, die sich in ihrem Risiko für Alzheimer-Krankheit unterscheiden.

Die Anwesenheit von Beta-Amyloid wurde durch einen Bluttest untersucht. Ein positiver Beta-Amyloid Test gilt als präsymptomatischer Indikator für die Alzheimer-Krankheit.

Aufgrund dieses Bluttests wurden die Patienten in zwei Gruppen eingeteilt. Es soll nun untersucht werden, ob sich die beiden in ihrer Gedächtnisleistung unterscheiden.

Dazu wurde der “Rey auditory verbal learning test” (Bean 2011) durchgeführt.

In diesem Test müssen Patienten zuerst eine Liste bestehend aus 15 Wörtern lernen. Sie werden danach mit 30 Wörtern getestet (15 alte, 15 neue Wörter) und müssen angeben, ob ein Wort auf der Liste war oder nicht (alt/neu).

Die Antworten der Patienten wurden bereits als als korrekte oder inkorrekte ‘Ja’-Antworten klassifiziert (hits und false alarms).

Packages laden

library(tidyverse)
library(patchwork)

Daten laden

d <- read_csv("data/amyloidSDT.csv")

Rows: 60 Columns: 6
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): group
dbl (5): ID, hit, miss, fa, cr

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Wir empfehlen, immer zuerst die Daten anzuschauen.

# A tibble: 60 × 6
      ID group      hit  miss    fa    cr
   <dbl> <chr>    <dbl> <dbl> <dbl> <dbl>
 1     1 Negative    13     2     0    15
 2     2 Negative    12     3     1    14
 3     3 Negative    14     1     0    15
 4     4 Negative    12     3     1    14
 5     5 Negative    11     4     2    13
 6     6 Negative    12     3     1    14
 7     7 Negative    10     5     2    13
 8     8 Negative    13     2     1    14
 9     9 Negative    12     3     0    15
10    10 Negative    12     3     2    13
# ℹ 50 more rows

Im Datensatz halben wir folgende Variablen:

ID: Patienten-ID
group: Indikator für Beta-Amyloid Bluttest (Negative oder Positive)
hit: Anzahl hits
miss: Anzahl misses
fa: Anzahl false alarms
cr: Anzahl correct rejections

Im Datensatz gibt es es einige Nullen – z.B. hat die Person mit der ID 1 keine False Alarms. Dies ist problematisch, weil wir die relative Häufigkeiten von Hits (hit_rate) und False Alarms (fa_rate) berechnen und diese anschliessend z-transformieren wollen. Die fa_rate ist der Anteil ‘Ja’-Antworten wenn das Wort tatsächlich gar nicht auf der Liste war, also fa / (fa + cr). Bei der ersten Person wäre dies 0/(0 + 15) = 0.

Das Problem ist nun, dass wir hier mit der relativen Häufigkeit eine Wahrscheinlichkeit schätzen - eine Wahrscheinlichkeit darf aber nicht \(0\) sein, sondern liegt zwischen \(-\infty\) und \(\infty\). Wenn wir qnorm() (die Quantilfunktion der Normalverteilung) auf den Wert \(0\) anwenden, erhalten wir:

qnorm(0)

[1] -Inf

Damit können wir nicht weiterrechnen. Wir wenden daher einen Trick an: wir addieren einfach zu jeder Zelle im Datensatz den Wert \(0.5\). Somit erhalten wir für die fa_rate der ersten Person:

0 + 0.5 / (0 + 0.5 + 15 + 0.5)

[1] 0.03125

Dies bedeutet, dass wir einen kleine Wahrscheinlichkeit erhalten; diese ist aber nicht Null. Diesen Wert können wir nun in qnorm() einsetzen.

qnorm(0.03125)

[1] -1.862732

Den Wert `0` ersetzen

add_half_count <- function(count) {
    count + 0.5
}

d <- d |>
    mutate(across(c(hit, miss, fa, cr), add_half_count))

# A tibble: 60 × 6
      ID group      hit  miss    fa    cr
   <dbl> <chr>    <dbl> <dbl> <dbl> <dbl>
 1     1 Negative  13.5   2.5   0.5  15.5
 2     2 Negative  12.5   3.5   1.5  14.5
 3     3 Negative  14.5   1.5   0.5  15.5
 4     4 Negative  12.5   3.5   1.5  14.5
 5     5 Negative  11.5   4.5   2.5  13.5
 6     6 Negative  12.5   3.5   1.5  14.5
 7     7 Negative  10.5   5.5   2.5  13.5
 8     8 Negative  13.5   2.5   1.5  14.5
 9     9 Negative  12.5   3.5   0.5  15.5
10    10 Negative  12.5   3.5   2.5  13.5
# ℹ 50 more rows

Hit und False Alarm Rate berechnen

d <- d |>
    mutate(
        hit_rate = hit / (hit + miss),
        fa_rate = fa / (fa + cr)
    )

Hit Rate vs False Alarm Rate

Bevor wir die SDT Kennzahlen berechnen, stellen wir die hit rate und false alarm rate grafisch dar:

d |>
      ggplot(aes(fa_rate, hit_rate, color = group)) +
      geom_abline(intercept = 0, slope = 1, linetype = 2) +
      geom_jitter() +
      scale_color_viridis_d(direction = -1, begin = 0.1, end = 0.8) +
      facet_wrap(~ group) +
      xlim(c(0, 1)) +
      theme_linedraw()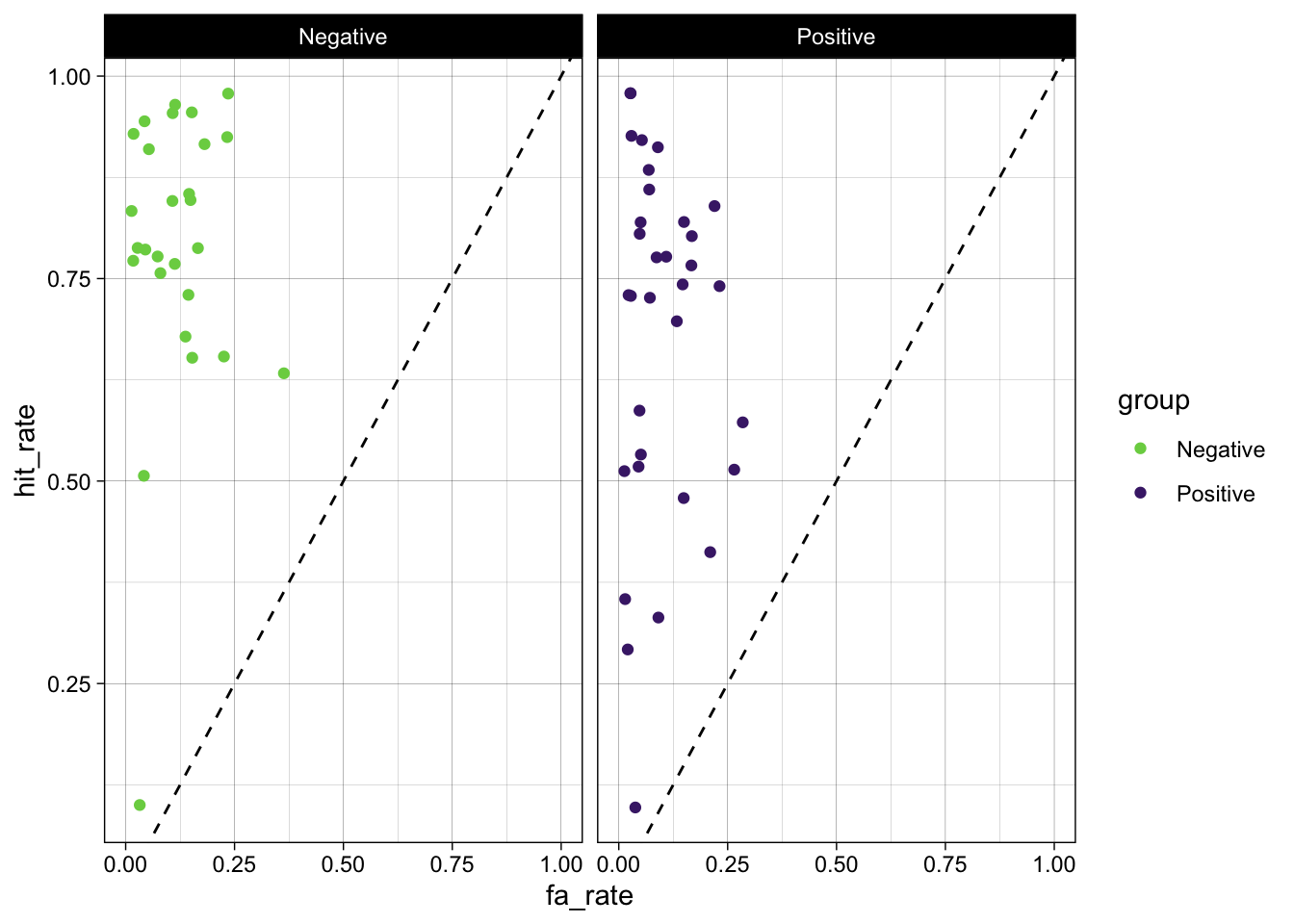

d’ und bias berechnen

d <- d |>
    mutate(
        zhr = qnorm(hit_rate),
        zfa = qnorm(fa_rate)
    )

d <- d |>
    mutate(
        dprime = zhr - zfa,
        k = -zfa,
        c = -0.5 * (zhr + zfa)
    )

Wir runden nun dprime, k und c auf zwei Nachkommastellen.

d <- d |>
    mutate(across(c(dprime, k, c), \(x) round(x, 2)))

# A tibble: 60 × 13
      ID group   hit  miss    fa    cr hit_rate fa_rate   zhr   zfa dprime     k
   <dbl> <chr> <dbl> <dbl> <dbl> <dbl>    <dbl>   <dbl> <dbl> <dbl>  <dbl> <dbl>
 1     1 Nega…  13.5   2.5   0.5  15.5    0.844  0.0312 1.01  -1.86   2.87  1.86
 2     2 Nega…  12.5   3.5   1.5  14.5    0.781  0.0938 0.776 -1.32   2.09  1.32
 3     3 Nega…  14.5   1.5   0.5  15.5    0.906  0.0312 1.32  -1.86   3.18  1.86
 4     4 Nega…  12.5   3.5   1.5  14.5    0.781  0.0938 0.776 -1.32   2.09  1.32
 5     5 Nega…  11.5   4.5   2.5  13.5    0.719  0.156  0.579 -1.01   1.59  1.01
 6     6 Nega…  12.5   3.5   1.5  14.5    0.781  0.0938 0.776 -1.32   2.09  1.32
 7     7 Nega…  10.5   5.5   2.5  13.5    0.656  0.156  0.402 -1.01   1.41  1.01
 8     8 Nega…  13.5   2.5   1.5  14.5    0.844  0.0938 1.01  -1.32   2.33  1.32
 9     9 Nega…  12.5   3.5   0.5  15.5    0.781  0.0312 0.776 -1.86   2.64  1.86
10    10 Nega…  12.5   3.5   2.5  13.5    0.781  0.156  0.776 -1.01   1.79  1.01
# ℹ 50 more rows
# ℹ 1 more variable: c <dbl>

Aggregierte Kennzahlen

se <- function(x) {
  sd(x) / sqrt(length(x))
}

dprimes <- d |>
  select(group, dprime) |> 
  group_by(group) |> 
  summarize(mean = mean(dprime),
            se = se(dprime))

cs <- d |> 
  select(group, c) |> 
  group_by(group) |> 
  summarize(mean = mean(c),
            se = se(c))

Grafische Darstellung von `d'` und `bias`

p_dprimes <- dprimes |>
  ggplot(aes(x=group, y=mean, group=1)) +
    geom_jitter(aes(group, dprime), alpha = 0.1, data = d, width = 0.05) +
    geom_line() +
    geom_errorbar(width=.1, aes(ymin=mean-se, ymax=mean+se), colour="black") +
    geom_point(shape=21, size=3, fill="white") +
    ylab("Sensitivity")

p_cs <- cs |>
    ggplot(aes(x=group, y=mean, group=1)) +
    geom_jitter(aes(group, c), alpha = 0.1, data = d, width = 0.05) +
    geom_line() +
    geom_errorbar(width=.1, aes(ymin=mean-se, ymax=mean+se), colour="black") +
    geom_point(shape=21, size=3, fill="white") +
    ylab("Bias")

p_dprimes + p_cs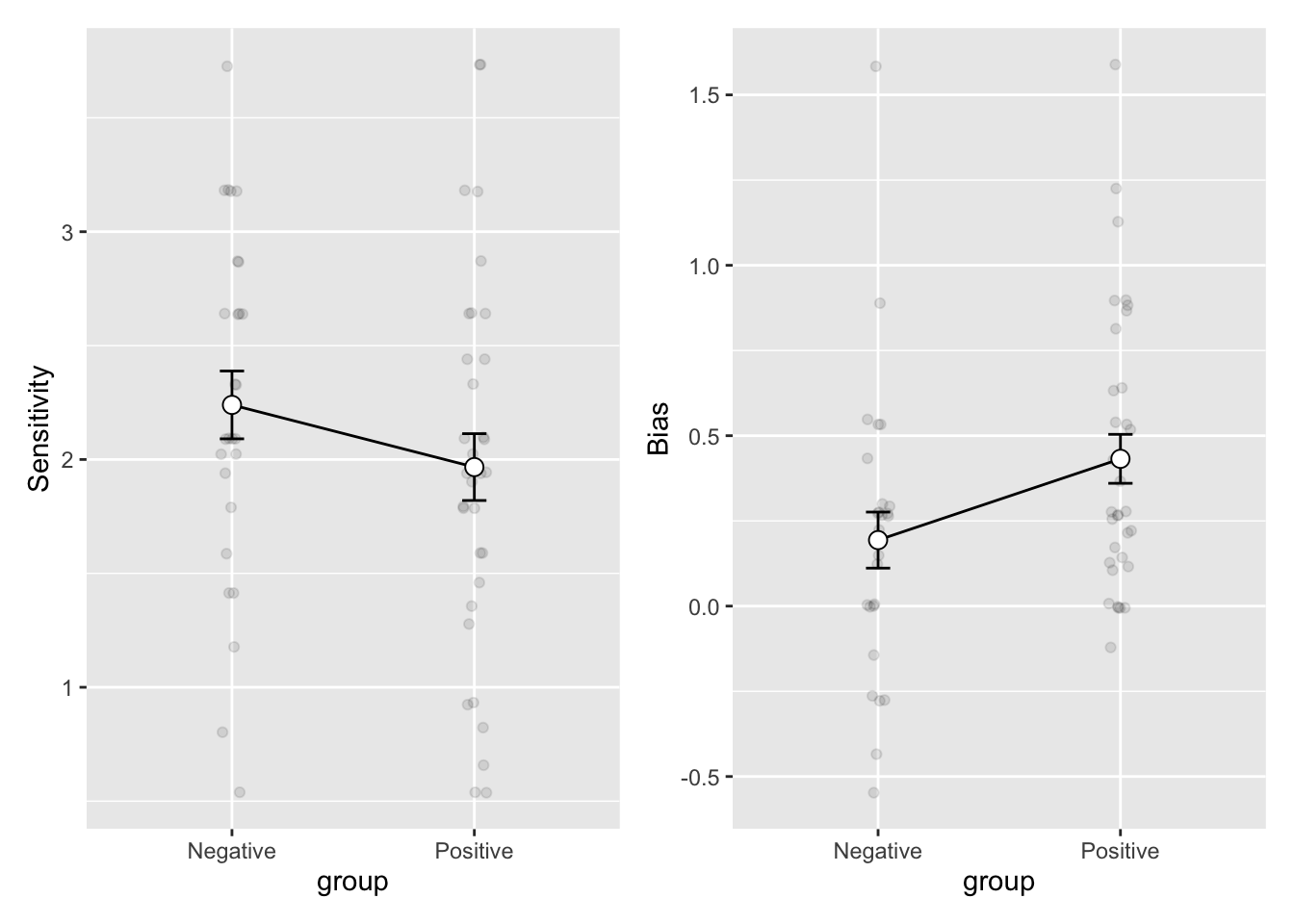

Fragen

Bitte versuchen Sie, folgende Fragen so gut wie möglich zu beantworten. Schreiben Sie Ihre Antworten direkt unter die Fragen.

Frage 1

Wie unterscheiden sich die Gruppen in der hit rate und false alarm rate (siehe erste Grafik)?

Antwort:

Frage 2

Wie unterscheidet sich die Sensitivität zwischen den Gruppen im RALVT? Was könnte das bedeuten? Denken Sie, dass der Unterschied von relevanter Grösse ist?

Antwort:

Frage 3

Wie unterscheidet sich die Antworttendenz zwischen den Gruppen im RALVT? Was könnte das bedeuten? Denken Sie, dass der Unterschied von relevanter Grösse ist?

Antwort:

Frage 4

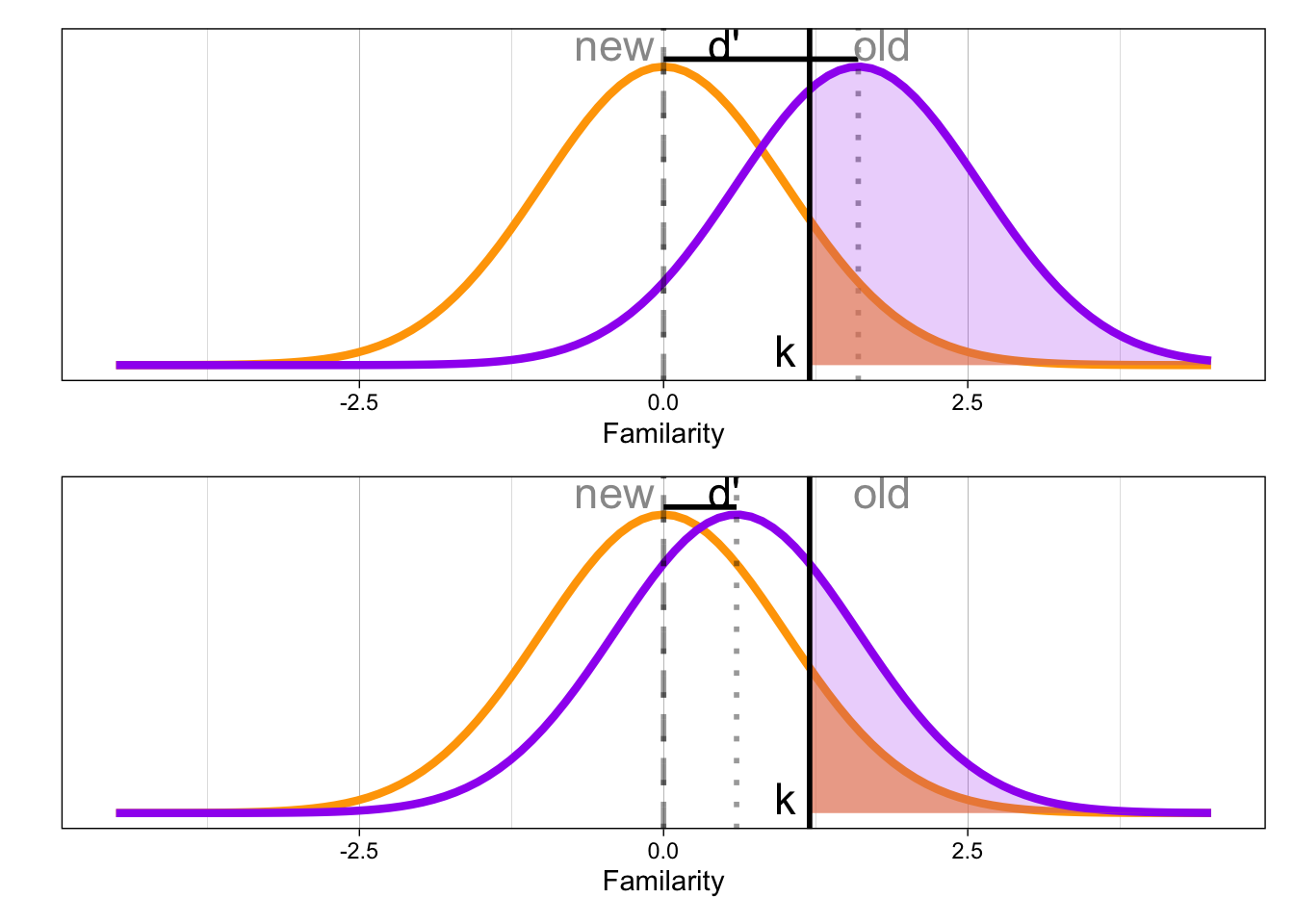
Wie denken Sie hängen Sensitivität und Antworttendenz in diesem Experiment zusammen? Was könnten die Gründe sein? Was passiert, wenn d’ kleiner wird, das Kriterium k aber konstant bleibt? Eventuell hilft diese Grafik, um darüber nachzudenken.

Fragen für Peer Review

Öffnen Sie das .Rmd-File und führen Sie es mit Knit oder von oben bis unten aus und schreiben Sie zu den Antworten eine Rückmeldung in ein Word/Text-File.

Hochladen

Laden Sie Ihr Peer Review anschliessend als Word/Text-File auf Ilias hoch.

References

Bean, Jessica. 2011. “Rey Auditory Verbal Learning Test, Rey AVLT.” In Encyclopedia of Clinical Neuropsychology, edited by Jeffrey S. Kreutzer, John DeLuca, and Bruce Caplan, 2174–75. New York, NY: Springer. https://doi.org/10.1007/978-0-387-79948-3_1153.

Reuse

https://creativecommons.org/licenses/by/4.0/

Citation

BibTeX citation:

@online{ellis2022,
  author = {Andrew Ellis and Gerda Wyssen},
  title = {Übung 4},
  date = {2022-05-05},
  url = {https://kogpsy.github.io/neuroscicomplabFS23//uebung-4-signal-detection.html},
  langid = {en}
}

For attribution, please cite this work as:

Andrew Ellis, and Gerda Wyssen. 2022. “Übung 4.” May 5, 2022. https://kogpsy.github.io/neuroscicomplabFS23//uebung-4-signal-detection.html.

Einleitung

Packages laden

Daten laden

Den Wert 0 ersetzen

Hit und False Alarm Rate berechnen

Hit Rate vs False Alarm Rate

d’ und bias berechnen

Aggregierte Kennzahlen

Grafische Darstellung von d' und bias

Fragen

Frage 1

Frage 2

Frage 3

Frage 4

Fragen für Peer Review

Hochladen

References

Reuse

Citation

Den Wert `0` ersetzen

Grafische Darstellung von `d'` und `bias`