Bayes Factors: Bayesianische Hypothesentests
Eine Alternative zu Null Hypothesis Significance Testing (NHST).
In der heutigen Sitzung:
- Modellvergleiche mit Bayes Factors
- Bayes Factors mit Jasp berechnen
Bayesian Inference in JASP: A Guide for Students: Einführung in die Bayesianische Statistik mit JASP (mit Datensätzen).
Ein sehr gutes Lehrbuch Statistik mit JASP: Learn Statistics with JASP. Enthält ein Kapitel zur Bayesianischen Statistik.
Keysers, C., Gazzola, V., & Wagenmakers, E.-J. (2020). Using Bayes factor hypothesis testing in neuroscience to establish evidence of absence. Nature Neuroscience, 23(7), https://doi.org/10.1038/s41593-020-0660-4
Absence of Evidence vs. Evidence of Absence
In den Neurowissenschaftler*innen ist es wichtig zu wissen, welche experimentellen Manipulationen einen Effekt haben. Genauso wichtig ist es jedoch zu wissen, welche Manipulationen keinen Effekt haben. Diese Frage zu beantworten ist jedoch mit traditionellen statistischen Ansätzen schwierig. Nicht signifikante Ergebnisse sind schwer zu interpretieren: Unterstützen sie die Nullhypothese oder sind sie einfach nicht informativ?
p-Werte sind schwierig zu erklären. Überlegen Sie sich nochmals, was man mit einem p-Wert genau aussagen kann.
Als Beispiel dient folgendes Experiment aus dem Paper von Keysers, Gazzola, and Wagenmakers (2020). Nehmen wir an, dass der vordere cinguläre Kortex (ACC) bei Ratten für die “emotionale Ansteckung” entscheidend ist und dass eine Deaktivierung des ACC durch lokale Injektion von Muscimol die emotionale Ansteckung im Vergleich zur Injektion von Kochsalzlösung verringern sollte.
Ein injiziertes Tier beobachtete, wie ein Artgenosse Elektroschocks erhielt, und die Erstarrung wurde als Mass für die emotionale Ansteckung gemessen. Es gab auch eine nicht-soziale Kontrollbedingung, bei der das injizierte Tier einem schock-konditionierten Ton ausgesetzt wurde. In einem solchen Experiment ist es wichtig zu zeigen, dass die Manipulation (Injektion von Muscimol) die emotionale Ansteckung reduziert, aber nicht die Erstarrung im Allgemeinen. Dies bedeutet, dass in der Kontrollbedingung keinen Unterschied zwischen den Injektionen von Muscimol und Kochsalzlösung geben sollte.
In diesem Kapitel lernen wir nun eine alternative Methode kennen, um Evidenz zu quantifizieren: Bayes Factors. Alternativ zu p-Werten bieten Bayes Factors Evidenz für oder gegen Hypothesen. Bayes Factors sind ein kontinuierliches Mass, welches im Prinzip angibt, um wieviel wir unsere Überzeugung für eine Hypothese ändern sollten, nachdem wir die Daten gesehen haben.
Bayesianische Statistik?
Wir wir in der letzten Sitzungen gehört haben, ist es wichtig, zwischen Parameterschätzung und Hypothesentest zu unterscheiden. Parameterschätzung bezeichnet den Prozess, einen oder mehrere Parameter in einem Modell zu schätzen. Um diese Schätzung durchzuführen, müssen wir eine a-priori-Verteilung der Parameterwerte angeben. Hypothesentesten ist einen Vergleich zwischen mehreren Modellen, welche sich in ihren a-priori-Verteilungen unterscheiden.
Zum Beispiel hatten wir im Kartenspiel verschiedene Vorannahmen über die Fähigkeiten der Spieler A und B. Eine Vorannahme drückte z.B. unsere Überzeugung aus, dass beide Spieler gleich gut waren, während eine andere Vorannahme die Überzeugung ausdrückte, dass entweder Spieler A oder Spieler B besser war. Diese Vorannahmen, zusammen mit unseren Annahmen über die Verteilung der Daten, bilden ein Modell \(\mathcal{M}\).
Bayesianische Parameterschätzung
In der Bayesianischen Parameterschätzung konzentrieren wir uns auf ein Modell \(\mathcal{M}\). Das Ziel unserer Inferenz ist die a-posteriori-Verteilung der Parameter \(\theta\), und wir können diese durch Anwendung von Bayes’ Theorem erhalten (unter Verwendung von Markov Chain Monte Carlo Sampling oder anderen Methoden).
\[ p(\theta | y) = p(\theta) \cdot \frac{p(y | \theta)}{p(y)} \]
Wir können die Bayes’sche Regel umformulieren, so dass die Abhängigkeit der Parameter \(\mathbf{\theta}\) vom Modell \(\mathcal{M}\) eindeutig wird: \[ p(\theta | y, \mathcal{M}) = \frac{p(y|\theta, \mathcal{M}) \cdot p(\theta | \mathcal{M})} {p(y | \mathcal{M})} \]
wo \(\mathcal{M}\) auf ein spezifisches Modell verweist. Dieses Modell wird durch die a-priori-Verteilung der Parameter \(p(\theta | \mathcal{M})\) und die Wahrscheinlichkeit der Daten \(p(y|\theta, \mathcal{M})\) bestimmt.
Die bedingte Wahrscheinlichkeit \(p(y | \mathcal{M})\) gibt nun die Wahrscheinlichkeit der Daten an, gemittelt über alle möglichen Parameterwerte unter der Vorverteilung im Modell \(\mathcal{M}\). Sie auch Modell-Evidenz genannt.
Bei der Parameterschätzung spielt \(p(y | \mathcal{M})\) nur die Rolle eines Normalisierungsfaktors. Beim Modellvergleich ist \(p(y | \mathcal{M})\) jedoch von zentraler Bedeutung.
Die Randwahrscheinlichkeit \(p(y | \mathcal{M})\) ist der Nenner aus der Bayes’schen Formel:
\[ p(\theta|y) = \frac{ p(y|\theta) * p(\theta) } {p(y)} \]
und ist gegeben durch: \[ p(y | \mathcal{M}) = \int{p(y | \theta, \mathcal{M}) p(\theta|\mathcal{M})d\theta} \]
Dies bedeutet, dass wir die Wahrscheinlichkeit der Daten \(p(y | \mathcal{M})\) erhalten, indem wir die Wahrscheinlichkeit der Daten für jeden möglichen Parameterwert \(\theta\) berechnen und dann über alle möglichen Parameterwerte mitteln.
Die a-priori-Verteilungen für \(\theta\) sind wichtig, da sie die Wahrscheinlichkeit möglicher Werte von \(\theta\) bestimmen.
Bayesianische Modellvergleiche
Nun wollen wir zwei verschiedene Modelle miteinander vergleichen – wir wollen wissen, welches Modell die Daten besser erklärt. Wir können die Bayes’sche Regel verwenden, um die Wahrscheinlichkeit der Modelle \(\mathcal{M1}\) und \(\mathcal{M2}\) zu berechnen (gemittelt über alle möglichen Parameterwerte innerhalb des Modells):
\[ p(\mathcal{M}_1 | y) = \frac{P(y | \mathcal{M}_1) p(\mathcal{M}_1)}{p(y)} \]
und
\[ p(\mathcal{M}_2 | y) = \frac{P(y | \mathcal{M}_2) p(\mathcal{M}_2)}{p(y)} \]
Eine Möglichkeit wäre, das Verhältnis der beiden Wahrscheinlichkeiten zu berechnen: \(p(\mathcal{M}_1 | y) / p(\mathcal{M}_2 | y)\). Dieses Verhältnis wird als posterior odds bezeichnet:
\[ \frac{p(\mathcal{M}_1 | y) = \frac{P(y | \mathcal{M}_1) p(\mathcal{M}_1)}{p(y)}} {p(\mathcal{M}_2 | y) = \frac{P(y | \mathcal{M}_2) p(\mathcal{M}_2)}{p(y)}} \]
\(p(y)\) können wir kürzen, da es in oberhalb und unterhalb des Bruchstriches im Nenner vorkommt. Wir erhalten:
\[ \frac{p(\mathcal{M}_1 | y) = P(y | \mathcal{M}_1) p(\mathcal{M}_1)} {p(\mathcal{M}_2 | y) = P(y | \mathcal{M}_2) p(\mathcal{M}_2)} \]
Auf der linken Seite haben wir das Verhältnis der a-posteriori Wahrscheinlichkeiten der beiden Modelle. Auf der rechten Seite haben wir das Verhältnis der Marginal Likelihoods der beiden Modelle, multipliziert mit den a-priori Wahrscheinlichkeiten jedes Modells. Die Marginal Likelihoods (auch bekannt als Modell-Evidenz) zeigen, wie gut jedes Modell die Daten erklärt.
Diese geben darüber Auskunft, wie wahrscheinlich die Daten sind, wenn wir alle möglichen Parameterwerte berücksichtigen. Die Marginal Likelihoods sind also die Wahrscheinlichkeit der Daten, gemittelt über alle möglichen Parameterwerte.
\[ \underbrace{\frac{p(\mathcal{M}_1 | y)} {p(\mathcal{M}_2 | y)}}_\text{Posterior odds} = \underbrace{\frac{P(y | \mathcal{M}_1)}{P(y | \mathcal{M}_2)}}_\text{Ratio of marginal likelihoods} \cdot \underbrace{ \frac{p(\mathcal{M}_1)}{p(\mathcal{M}_2)}}_\text{Prior odds} \]
\(\frac{p(\mathcal{M}_1)}{p(\mathcal{M}_2)}\) sind nun die Prior Odds, und \(\frac{p(\mathcal{M}_1 | y)}{p(\mathcal{M}_2 | y)}\) sind die Posterior Odds. Diese sagen uns, welches Modell wir a-priori und a-posteriori für wahrscheinlicher halten. Da unsere a-priori Überzeugungen aber subjektiv sein können, sind wir eigentlich nur an dem Verhältnis der marginalen Likelihoods interessiert. Wir können annehmen, dass a-priori die beiden Modelle gleichwahrscheinlich sind; das heisst, wir setzen die Prior Odds auf 1 setzen. So erhalten wir
\[ \frac{P(y | \mathcal{M}_1)}{P(y | \mathcal{M}_2)} \]
Dies ist der Bayes Factor. Falls \(P(y | \mathcal{M}_1)\) grösser ist als \(P(y | \mathcal{M}_2)\), dann ist der Bayes Factor grösser als 1. Falls \(P(y | \mathcal{M}_1)\) kleiner ist als \(P(y | \mathcal{M}_2)\), dann ist der Bayes Factor kleiner als 1. Der Bayes Factor gibt also direkt an, welches Modell die Daten besser erklärt.
Wenn wir zwei Modelle \(\mathcal{M}_1\) und \(\mathcal{M}_2\) vergleichen, wird der Bayes Factor oftmals so geschrieben:
\[ BF_{12} = \frac{P(y | \mathcal{M}_1)}{P(y | \mathcal{M}_2)}\]
\(BF_{12}\) ist also der Bayes Factor für \(\mathcal{M}_1\) und gibt an um wieviel \(\mathcal{M}_1\) die Daten besser “erklärt”.
Als Beispiel, wenn wir ein \(BF_{12} = 5\) erhalten, bedeutet dies, dass die Daten 5 Mal wahrscheinlicher unter Modell 1 als unter Modell 2 aufgetreten sind. Umgekehrt, wenn \(BF_{12} = 0.2\), dann sind die Daten 5 Mal wahrscheinlicher unter Modell 2 aufgetreten.
Wenn wir \(BF_{12} = 0.2\) erhalten, ist es einfacher, Zähler und Nenner zu vertauschen:
\[ BF_{21} = \frac{P(y | \mathcal{M}_2)}{P(y | \mathcal{M}_1)}\]
Die folgenden Interpretationen von Bayes Factors werden manchmal verwendet, obwohl es nicht wirklich notwendig ist, diese zu klassifizieren. Bayes Factors sind ein kontinuierliches Mass für Evidenz.
Hypothesentesten
Wir führen oft Modellvergleiche zwischen einer Nullhypothese \(\mathcal{H}_0\) und einer alternativen Hypothese \(\mathcal{H}_1\) durch (Die Begriffe “Modell” und “Hypothese” werden synonym verwendet). Eine Nullhypothese bedeutet, dass wir den Wert des Parameters auf einen bestimmten Wert festlegen, z.B. \(\theta = 0.5\). Die alternative Hypothese bedeutet, dass wir den Wert des Parameters nicht festlegen, sondern eine a-priori Verteilung annehmen.
Im Gegensatz zu NHST muss die Alternativhypothese spezifiziert werden. Mit anderen Worten, die Parameter müssen eine a-priori Verteilung erhalten.
In JASP werden Bayes Factors (BF) so berichtet:
\[ BF_{10} = \frac{P(y | \mathcal{H}_1)}{P(y | \mathcal{H}_0)}\]
Dies ist ein BF für eine ungerichtete Alternative \(\mathcal{H}_1\) gegen die Nullhypothese \(\mathcal{H}_0\). Wenn wir einen gerichteten Test durchführen, dann wird der BF entweder so (\(>0\)):
\[ BF_{+0} = \frac{P(y | \mathcal{H}_+)}{P(y | \mathcal{H}_0)}\]
oder so (\(<0\)) berichtet. \[ BF_{-0} = \frac{P(y | \mathcal{H}_-)}{P(y | \mathcal{H}_0)}\]
Wenn wir nun einen BF für die Nullhypothese wollen, können wir einfach den Kehrwert von \(BF_{10}\) nehmen:
\[ BF_{01} = \frac{1}{BF_{10}}\]
Wenn wir zwei genestete Modelle vergleichen, d.h. ein Modell mit 1 freiem Parameter und ein Nullmodell (in dem dieser Parameter auf einen bestimmten Wert festgelegt ist), können wir das Savage-Dickey Density Ratio verwenden, um den Bayes-Faktor zu berechnen.
Nullmodell (\(\mathcal{H}_0\) or \(\mathcal{M}_0\)): \(\theta = \theta_0\)
Alternativmodell (\(\mathcal{H}_1\) or \(\mathcal{M}_1\)): \(\theta \neq \theta_0\)
\(\theta\) braucht unter \(\mathcal{H}_1\) eine a-priori Verteilung. Im Kartenspiel-Beispiel vom letzten Kapitel war dies eine Beta-Verteilung mit \(\alpha = 1\) und \(\beta = 1\): \(\theta \sim \text{Beta}(1, 1)\). Diese Hypothese besagt, dass alle Parameterwerte gleich wahrscheinlich sind.
Das Savage-Dickey Density Ratio ist eine verinfachte Methode, um einen Bayes Factor zu erhalten - wir müssen einfach \(\mathcal{M}_1\) betrachten, und die a-posterior Verteilung durch die a-prior Verteilung an der Stelle \(\theta_0\) teilen.
Als Beispiel: stellen Sie sich vor, dass eine Person 9 von 10 Ja/Nein Fragen korrekt beantwortet.
n_correct <- 9
n_questions <- 10Wir wollen wissen: wie wahrscheinlich ist es, dass die Person geraten hat (\(\theta=0.5\))?
Wir nehmen nun eine uniforme a-priori Verteilung für \(\theta\) an: \[ p(\theta) = Beta(1, 1) \]
pd <- tibble(
x = seq(0, 1, by = .01),
Prior = dbeta(x, 1, 1)
)
ggplot(pd, aes(x, Prior)) +
geom_line(linewidth = 1.5) +
coord_cartesian(xlim = 0:1, ylim = c(0, 6), expand = 0.01) +
labs(y = "Density", x = bquote(theta))
Im nächsten Schritt wenden wir Bayes Theorem an, um die a-posteriori Verteilung zu erhalten:
\[ p(\theta|y) = Beta(1 + 9, 1 + 1) \]
Unser “Test-Wert” ist \(θ = 0.5\). Wir können nun sowohl die a-priori als auch die a-posteriori Verteilung an dieser Stelle auswerten:
Prior:
(dprior <- dbeta(0.5, 1, 1))[1] 1Posterior:
(dposterior <- dbeta(0.5, 10, 2))[1] 0.1074219Der Bayes Factor für die Nullhypothese \(BF_{01}\) ist die Wahrscheinlichkeit der a-posteriori Verteilung geteilt durch die Wahrscheinlichkeit der a-priori Verteilung an der Stelle \(\theta_0\):
BF01 <- dposterior / dpriorBF01[1] 0.1074219Da eine Zahl \(<0\) nicht so leicht interpretierbar ist, berechnen wir \(BF_{10}\):
(BF10 <- 1/BF01)[1] 9.309091Die Daten (9 von 10 Fragen richtig beantwortet) sind also \(9.3\) mal wahrscheinlicher unter der Alternativhypothese als unter der Nullhypothese.
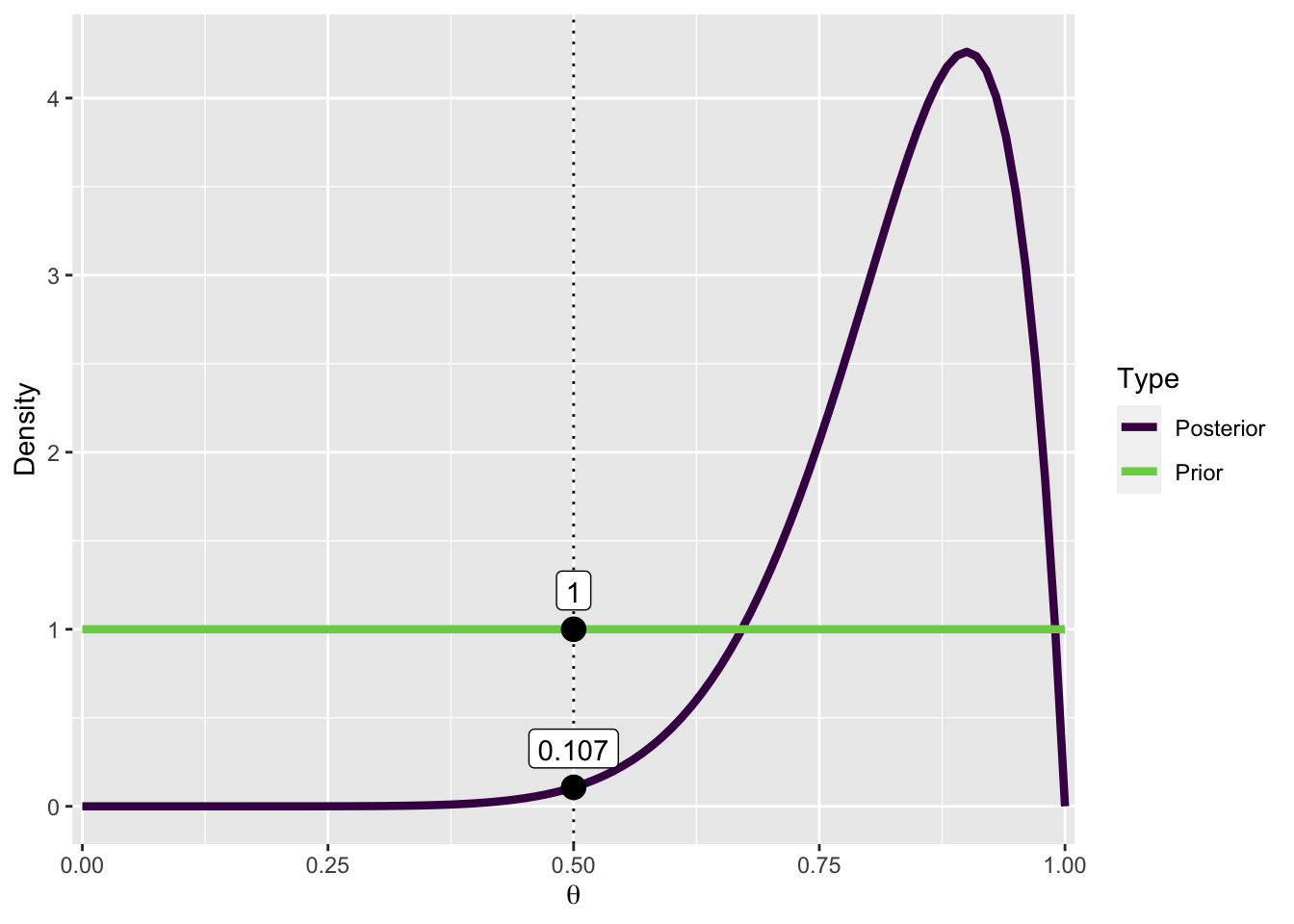
In JASP wird der BF folgendermassen grafisch dargestellt. Wir plotten sowohl die a-priori als auch die a-posteriori Verteilung, und die Wahrscheinlichkeitsdichten an der Stelle \(\theta_0 = 0.5\).
Die Wahrscheinlichkeitsdichte von \(\theta_0\) wird kleiner, nachdem wir die Daten berücksichtigt haben. Anders formuliert: Die Wahrscheinlichkeit von \(\theta_0\) hat abgenommen, nachdem wir die Daten beobachtet haben. Dies ermöglicht uns zu schlussfolgern, dass die Daten (9 von 10) etwa 9 Mal wahrscheinlicher unter \(\mathcal{M_1}\) sind.
pd <- pd |>
mutate(Posterior = dbeta(x, 1 + n_correct, 1 + (n_questions-n_correct)))
pdw <- pd |>
pivot_longer(names_to = "Type",
values_to = "density",
Prior:Posterior)
pdw |>
ggplot(aes(x, density, col = Type)) +
geom_vline(xintercept = 0.5, linetype = "dotted") +
geom_line(linewidth = 1.5) +
scale_x_continuous(expand = expansion(0.01)) +
scale_color_viridis_d(end = 0.8) +
labs(y = "Density", x = bquote(theta)) +
annotate("point", x = c(.5, .5),
y = c(pdw$density[pdw$x == .5]),
size = 4) +
annotate("label",
x = c(.5, .5),
y = pdw$density[pdw$x == .5],
label = round(pdw$density[pdw$x == .5], 3),
vjust = -.5
)
Eine Student*in beantwortet 9 von 10 Fragen korrekt.
- Was ist die Evidenz dafür, dass die Student*in geraten hat (Glück hatte)?
- Was ist die Evidenz dafür, dass die Wahrscheinlichkeit einer korrekten Antwort der Student*in grösser als \(0.5\) ist?
Importieren Sie den Datensatz ExamQuestions.csv ins JASP und führen Sie einen Bayesian binomial rate test durch.
Bayesian t-Test
Um einen Bayesianischen t-Test durchzuführen, müssen wir ebenfalls Parameter schätzen, und zwei Modelle miteinander vergleichen. Dies werden wir anhand zweier Beispiele in JASP demonstrieren.
In diesem Beispiel möchten wir die IQ-Werte von zwei Gruppen vergleichen. Einer der Gruppen wurde ein Medikament zur Steigerung der Intelligenz verabreicht, die andere ist die Kontrollgruppe.
Importieren Sie den Datensatz SmartDrug.csv ins JASP und führen Sie einen Bayesian t-test durch.
Öffnen Sie den Datensatz Eye Movements in JASP: Open > Data Library > T-Tests > Eye Movements. In diesem Datensatz wird die Anzahl erinnerter Wörter zwischen zwei Gruppen verglichen. In der einen Gruppe wurden die Probanden instruiert, während der Erinnerungsphase auf einen zentralen Punkt zu fixieren; in der anderen Gruppe wurden die Probanden instruiert, horizontale Sakkaden auszuführen.
Eine sehr gute interaktive Visualisierung eines Bayesian two-sample t test finden Sie unter folgendem Link: 👉 rpsychologist.com/d3/bayes.
References
Reuse
Citation
@online{ellis2022,
author = {Andrew Ellis},
title = {Bayes {Factors:} {Bayesianische} {Hypothesentests}},
date = {2022-05-15},
url = {https://kogpsy.github.io/neuroscicomplabFS23//bayesian-statistics-3.html},
langid = {en}
}