10. Sitzung

Evidence accumulation models: II

Andrew Ellis

Neurowissenschaft Computerlab FS 22

2022-05-03

1

Simulating RT and choice data

Simulating RT and choice data

Load library

Show code 
library(rtdists)

Parameters

Mit rdiffusion() können wir ein Experiment simulieren, bei dem die Fehler im Schnitt schneller als die korrekten Antworten sind, indem wir eine A Priori Präferenz für die Untergrenze definieren (z = 0.2).

Die 5 wichtigsten Argumente der Funktion sind:

n: Anzahl Zufallszahlen
a: boundary separation
v: drift rate
t0: non-decision time
z: bias

Simulate

Show code 
rts <- rdiffusion(500, a = 1, v = 2, t0 = 0.5, z = 0.2)

glimpse(rts)
Rows: 500
Columns: 2
$ rt       <dbl> 0.8207971, 0.5871117, 0.8568052, 0.5875147, 0.5460999, 0.5883…
$ response <fct> lower, upper, upper, upper, lower, lower, upper, upper, upper…
Show code 
head(rts)
         rt response
1 0.8207971    lower
2 0.5871117    upper
3 0.8568052    upper
4 0.5875147    upper
5 0.5460999    lower
6 0.5883296    lower

Grafisch darstellen

Show code 
rts |> 
  ggplot(aes(rt, response, fill = response)) +
  geom_violin() +
  geom_jitter(height = 0.1, alpha = 0.5) +
  scale_fill_viridis_d(option = "B", direction = -1, 
                       begin = 1/3, end = 3/3) +
  xlim(c(0, 2))

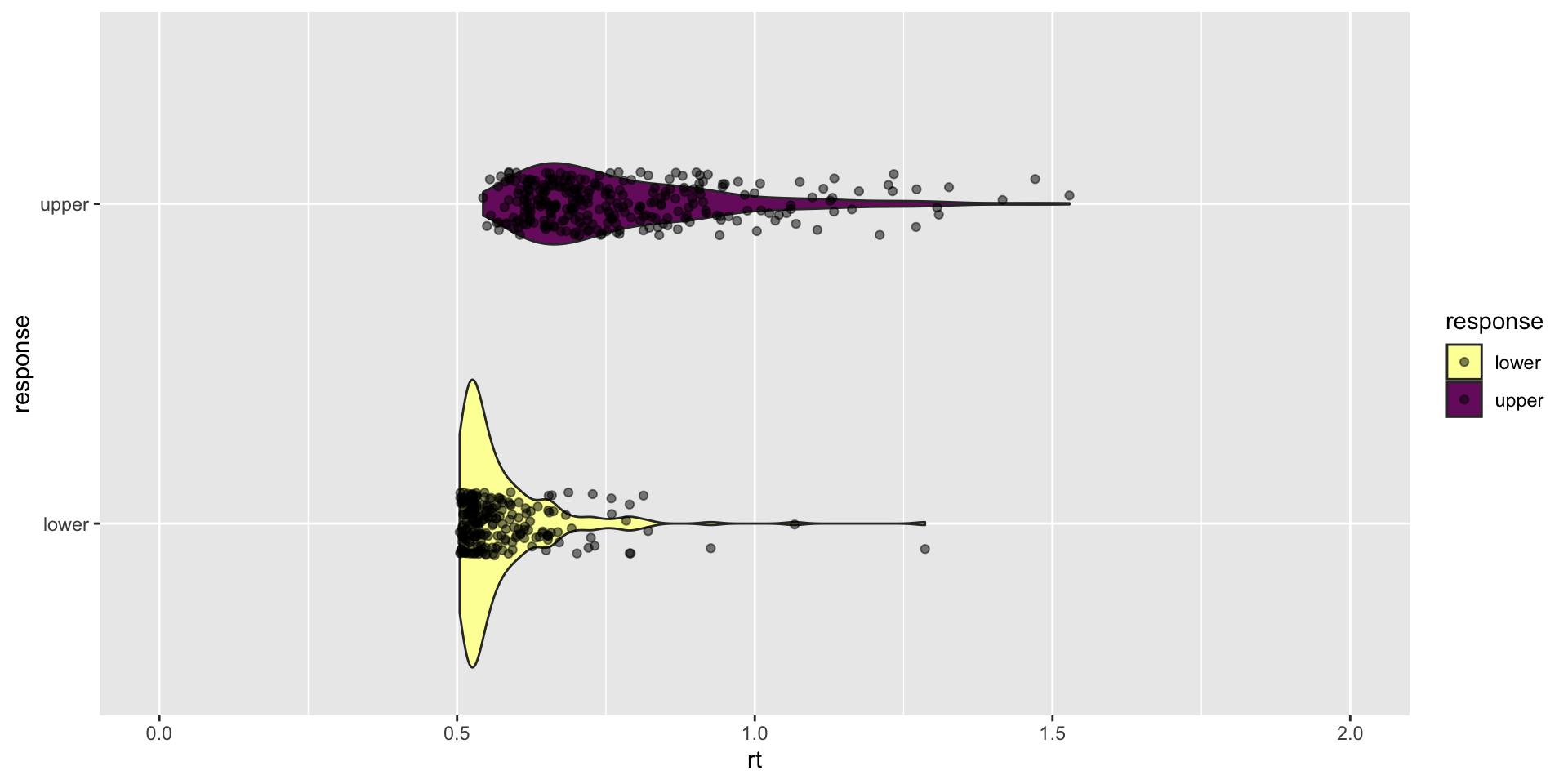
Effect of Bias

Show code 
d <- bind_rows(
  rdiffusion(500, a = 2, v = 1.5, t0 = 0.2, z = 0.5) |> 
  mutate(type = "unbiased"),
  rdiffusion(500, a = 2, v = 1.5, t0 = 0.2, z = 0.2) |> 
  mutate(type = "biased"))
Show code 
d |> 
  ggplot(aes(rt, response, fill = response)) +
  geom_violin() +
  geom_jitter(height = 0.1, alpha = 0.5) +
  scale_fill_viridis_d(option = "B", direction = -1, 
                       begin = 1/3, end = 3/3) +
  xlim(c(0, 2)) +
  facet_wrap(~type, ncol = 1)

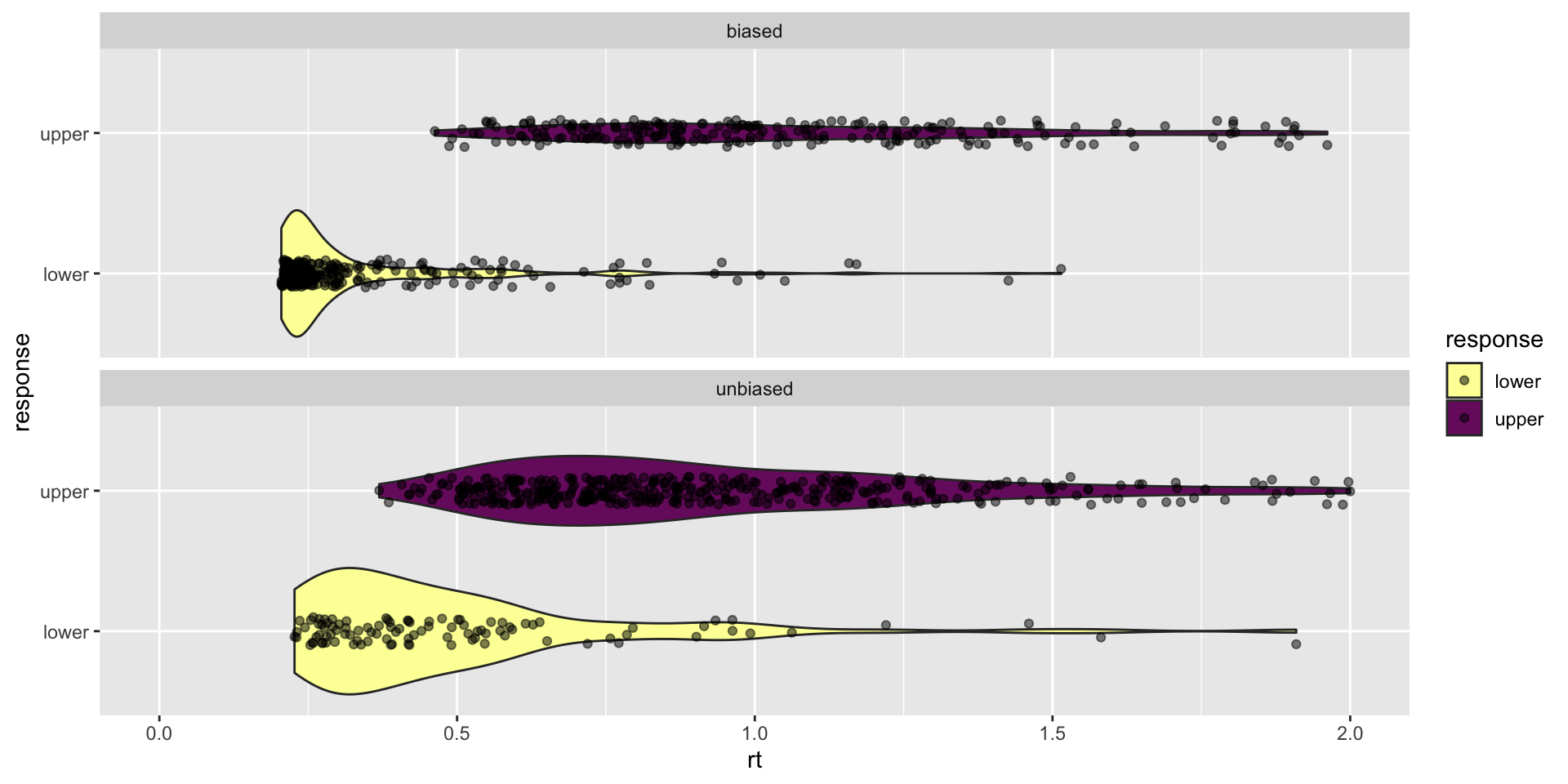
Zusammenfassen

Show code 
rts |> 
    group_by(response) |> 
    summarise(mean = mean(rt),
              median = median(rt),
              sd = sd(rt))
# A tibble: 2 × 4
  response  mean median     sd
  <fct>    <dbl>  <dbl>  <dbl>
1 lower    0.574  0.543 0.0913
2 upper    0.779  0.720 0.181

2

Maximum likelihood estimation

Maximum Likelihood Schätzung

  • Die Likelihood - genauer gesagt die Likelihood-Funktion - ist eine Funktion, die angibt, wie wahrscheinlich es ist, einen bestimmten Satz von Beobachtungen mit einem bestimmten Modell zu erhalten.

  • Wir betrachten die Menge der Beobachtungen (Daten) als gegeben.

  • Nun überlegen wir, bei welchem Satz von Modellparametern wir die Daten am wahrscheinlichsten beobachten würden.

Wahrscheinlichkeit der Daten

Wenn wir eine Reihe von Datenpunkten haben (wie es in der Regel bei psychologischen Experimenten der Fall ist), können wir eine gemeinsame Wahrscheinlichkeit oder Wahrscheinlichkeitsdichte für die Daten in einem Datenvektor y erhalten, indem wir die einzelnen Wahrscheinlichkeiten oder Wahrscheinlichkeitsdichten miteinander multiplizieren, wobei wir davon ausgehen, dass die Beobachtungen in y unabhängig sind:

\[ f(\bf{y}|\bf{\theta} = \prod^k{f(y_k | \bf{\theta})}) \]

  • \(k\) indiziert die Datenpunkte \(y_k\) im Vektor \(\bf{y}\).

Likelihood Funktion

Der Unterschied zwischen Wahrscheinlichkeit und Likelihood besteht darin, dass wir uns hier für die verschiedenen mögliche Parameterwerte beziehen, und die Likelihood-Funktion sagt uns, wie wahrscheinlich jeder dieser Parameterwerte angesichts der von uns beobachteten Daten ist.

\[ L(\bf{\theta} | \bf{y}) = \prod^k{L(\bf{\theta} | y_k}) \]

Beisiel: Binomial likelihood

Wir werfen eine Münze:

  • zwei mögliche Ergebnisse (Kopf und Zahl),
  • feste Anzahl von “Versuchen” (100 Münzwürfe)
  • feste Wahrscheinlichkeit für “Erfolg” (d. h. Kopf)
Show code 
set.seed(91)

heads <- rbinom(1, 100, 0.5)
heads
[1] 48

Wahrschienlichkeit der Daten gegeben \(p = 0.6\)

Show code 
biased_prob <- 0.6

# Using R's dbinom function (density function for a given binomial distribution)
dbinom(heads, 100, biased_prob)
[1] 0.004244495

Beispiel Kartenspiel zwischen 2 Spielern

  • Spieler A gewinnt 6 Mal in 9 Spielen:
Show code 
wins <- 6
games <- 9
  • Wir definieren einen Vektor mit 100 möglichen Parameterwerten:
Show code 
n_points <- 100
p_grid <- seq( from=0.001 , to=0.999 , length.out = n_points )
  • Nun berechnen wir die Wahrscheinlichkeit der Daten, gegeben die Parameterwerte:
Show code 
likelihood <- dbinom(wins, size = games , prob = p_grid)

Beispiel Kartenspiel zwischen 2 Spielern

Show code 
plot(p_grid , likelihood, type="l", main="Likelihood", col = "firebrick3", lwd = 2)
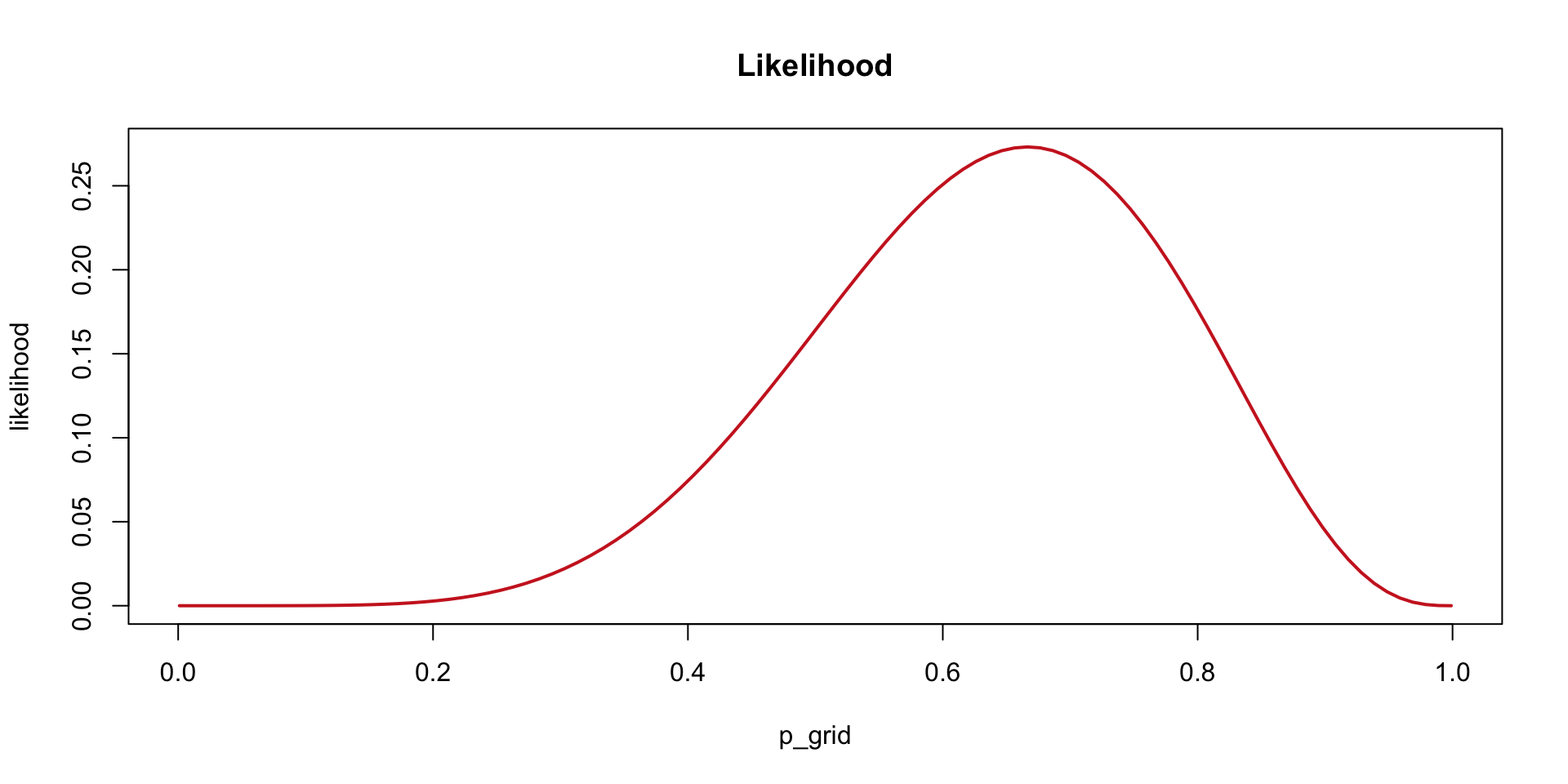
  • Index des Parameterwertes, welcher die Likelihood maximiert:
Show code 
which.max(likelihood)
[1] 67
  • Parameterwert andiesem Index:
Show code 
p_grid[which.max(likelihood)]
[1] 0.6663333

MLE: Negative Log Likelihood minimieren

  • Definiere eine Funktion, welche die negative log Wahrscheinlichkeitsfunktion für einen bestimmten Wert von p berechnet.
  • Suche nach dem Wert von p, für den diese Funktion minimiert wird.

Binomial Likelihood

\[ f(k | p_{heads}, N) = \binom{N}{k} p_{heads}^k (1-p_{heads}^{N-k}) \] \[ lnL(\bf{\theta} | \bf{y}) = \sum^k_{k=1}{ln L(\bf{\theta} | y_k}) \]

Funktion definieren

Show code 
loglik <- function(p){
  likelihoods <- dbinom(heads, 100, p)
   return(-sum(log(likelihoods)))
}

Minimieren

Show code 
nlm(loglik, 0.1, stepmax=0.1)
$minimum
[1] 2.530081

$estimate
[1] 0.4799995

$gradient
[1] 0

$code
[1] 1

$iterations
[1] 8

🏠 Neurowissenschaft Computerlab FS22